図学講義B
Graphic Science B

From April 2020 -- To August 2020
CAD Training Room (B308)
The Center for Education in Liberal Arts and Sciences, Osaka University

図学は空間内の立体の加工・操作によって生じる形状や位置関係を作図によって求めるための解析手法であり、図法幾何学とも呼ばれる。この授業は専門教育の設計科目で必須となる各種投影法の基礎知識と３次元形態の解析に必要な知識の習得を目的とする。ここで扱う投影法は正投影、斜投影、軸測投影、標高投影、透視投影とし、3次元形態の解析では図法幾何学を基本に、切断、相貫、回転、陰影、副投影等について講義する。
Graphic Science, which is also called descriptive geometry, is an analytical method to find shapes and positional relationships of solids in space by processes and operations with the drawings. This class aims to acquire the basic knowledge of various projection methods which are indispensable for the design subjects in professional education and the knowledge necessary for analysis of three-dimensional forms. The projection methods used in this class are orthogonal projection, oblique projection, axonometric projection, indexed projection, and perspective projection. The three-dimensional form analytical methods are cutting, intersection, revolution, shade and shadow, auxiliary projection, etc. based on descriptive geometry.

本授業で用いる教科書：実用図学（共立出版）ISBN：978-4-320-11432-6

第1章　平面
1. 1 図形を構成する基本的な要素
1. 2 多角形
1. 3 曲線
1. 4 平面充填
1. 5 平面図形の作図

第2章　立体
2. 1 多面体
2. 2 空間曲線
2. 3 曲面
2. 4 建築や人工物との関係

第3章　立体から平面へ

3次元の立体を2次元の紙上（平面）に表現する方法を「投象」と呼ぶ。これは平たく言えば，「図の描き方」である。この章では投象の種類，それぞれの投象の特色（長所と短所），考え方や作図の基本を概説する。

3.1 投象の分類
図学における「投象」は、3次元空間にある立体図形を2次元平面上に映し取る操作であり、主として「平行投象」と「中心投象」が用いられる。平行投象は、空間にある点と投象する平面（投象面）上の点を結んだ「投射線」が互いに平行な投象のことである。中心投象は投射線が一つの点（投象中心）から放射する投象のことであり、「透視投象」ともいう。

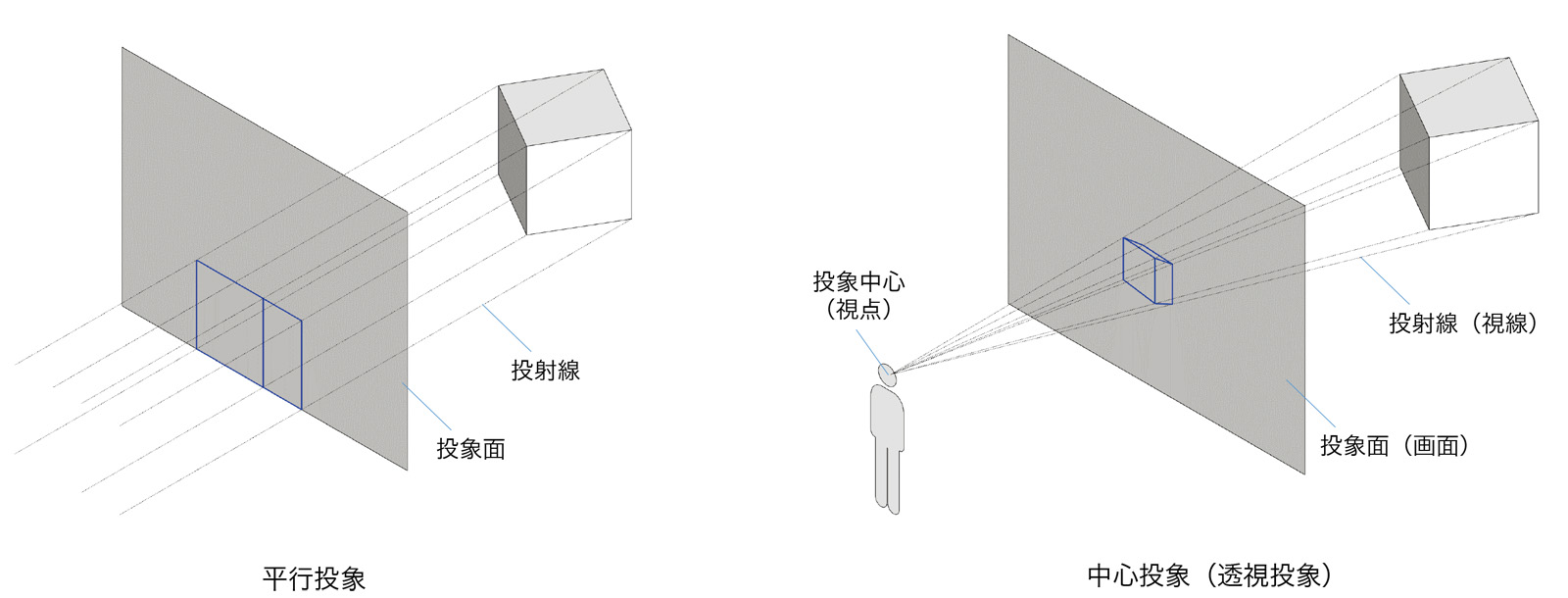
平行投象は、投射線が投象面に垂直な「垂直投象」と、投射線が投象面に斜交する「斜投象」に分類できる。垂直投象には「正投象」「標高投象」「軸測投象」などが含まれている。また、複数の図で立体を表現する「複面投象」と1枚の図で立体を表現する「単面投象」にも分類できる。以下に投象の種類とそれぞれの投象で描かれた事例をまとめる。

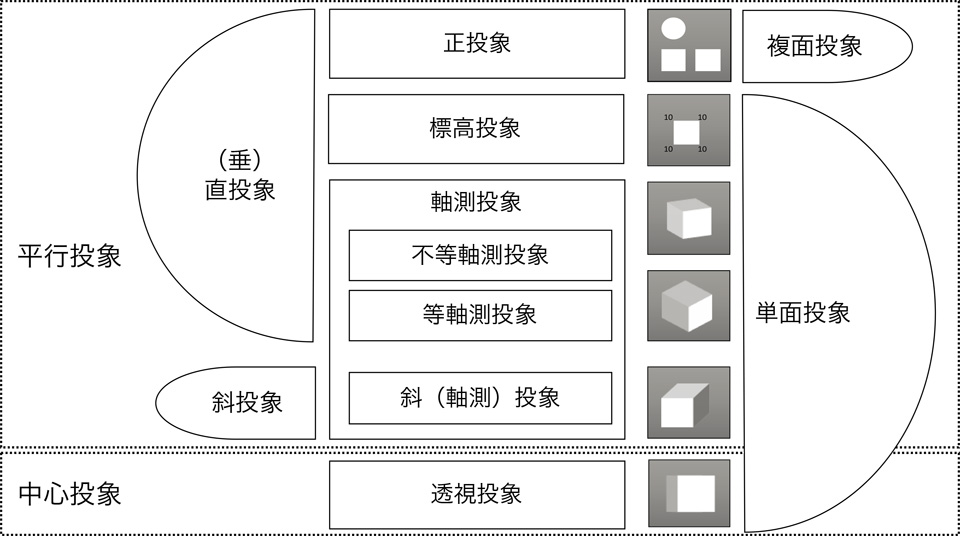
各投象の事例紹介

3.2 各投象の作図
1) 正投象/orthographic projection

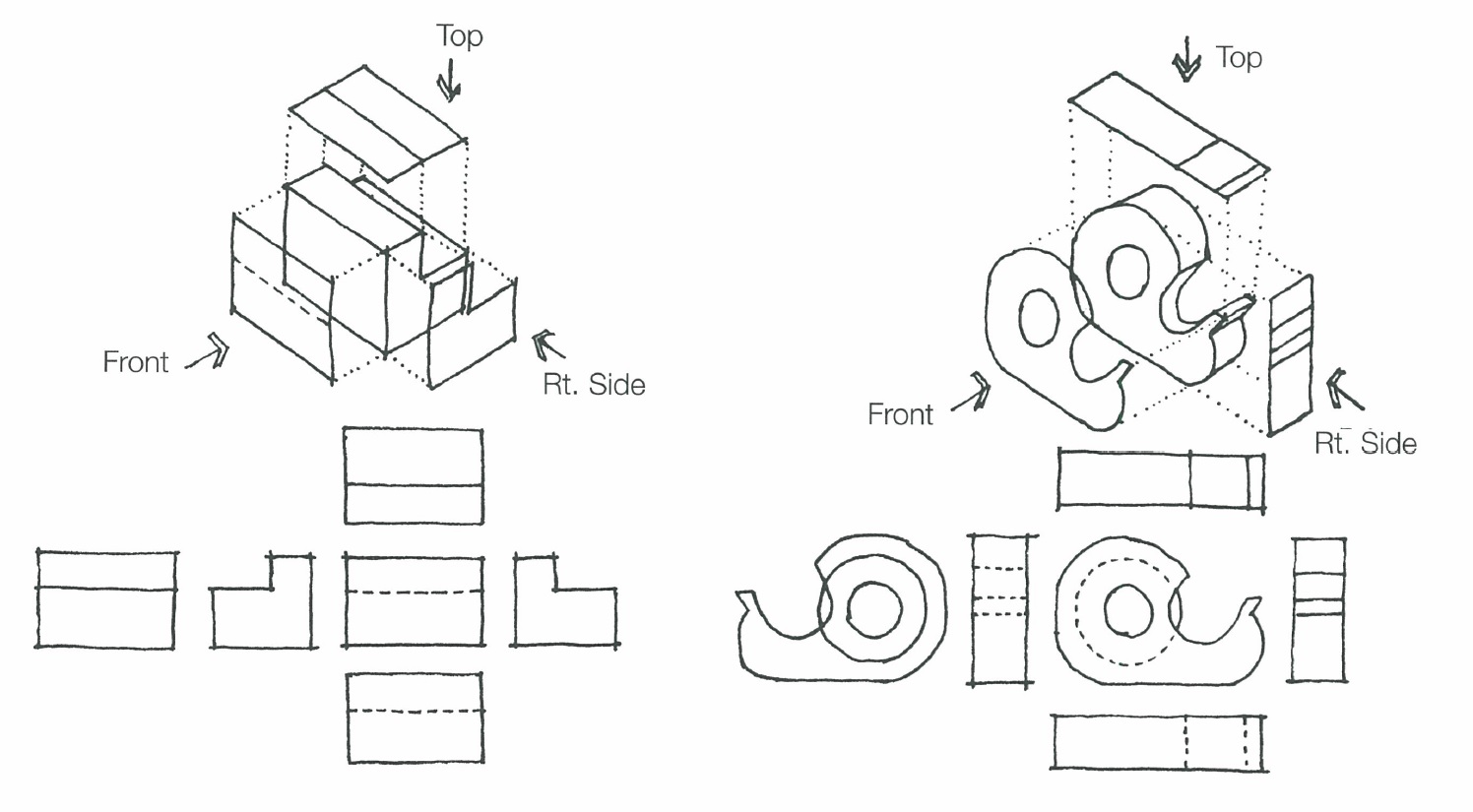
正投象は平行投象の最も基本となる投象で投象面に垂直な投射線によって作図される。立体を正確に描き表すにあたって基本となる投象であり設計図面に用いられる。。

正投象　 ↑

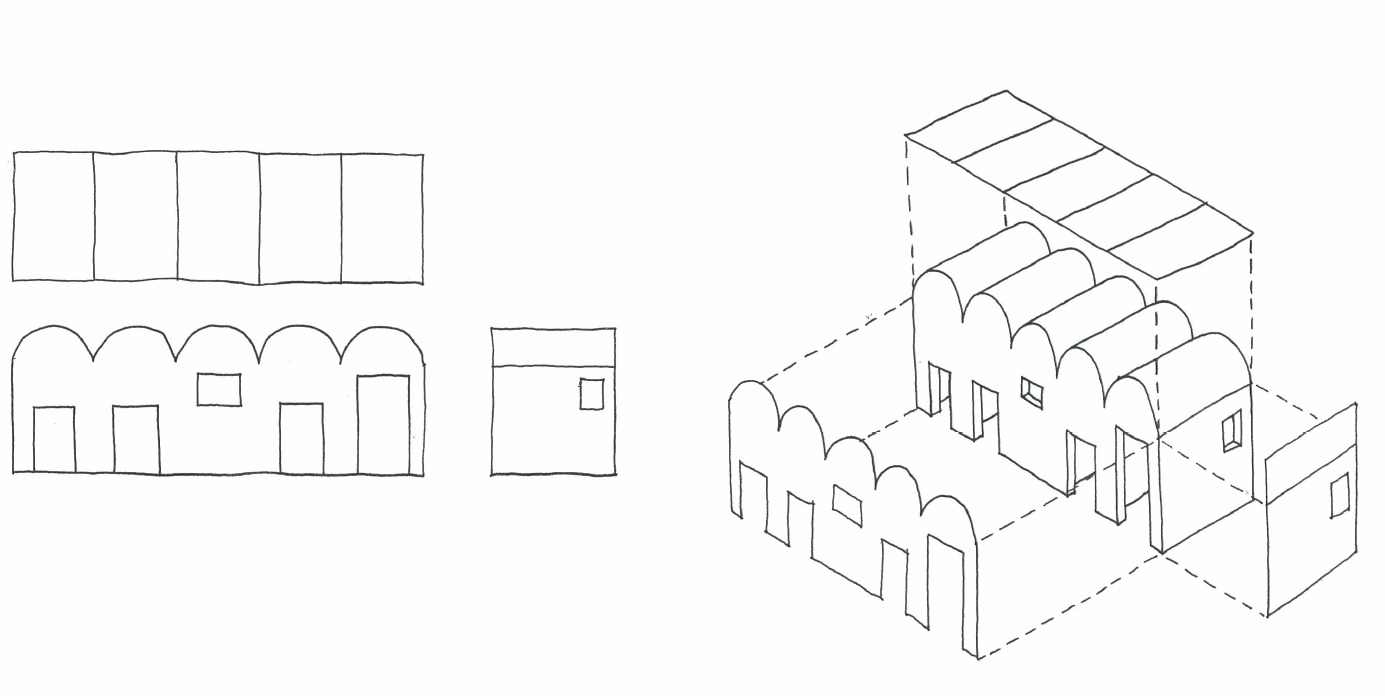
2) 斜投象/oblique projection
直交3軸を投象面に傾けて平行投象し、3軸を目安に立体図形を描く方法を「軸測投象」という。軸測投象の中で、投射線と投象面が斜交する場合を「斜投象」という。斜投象は、作図法が理解し易く、一般の人が見取り図を描くのによく用いられる。

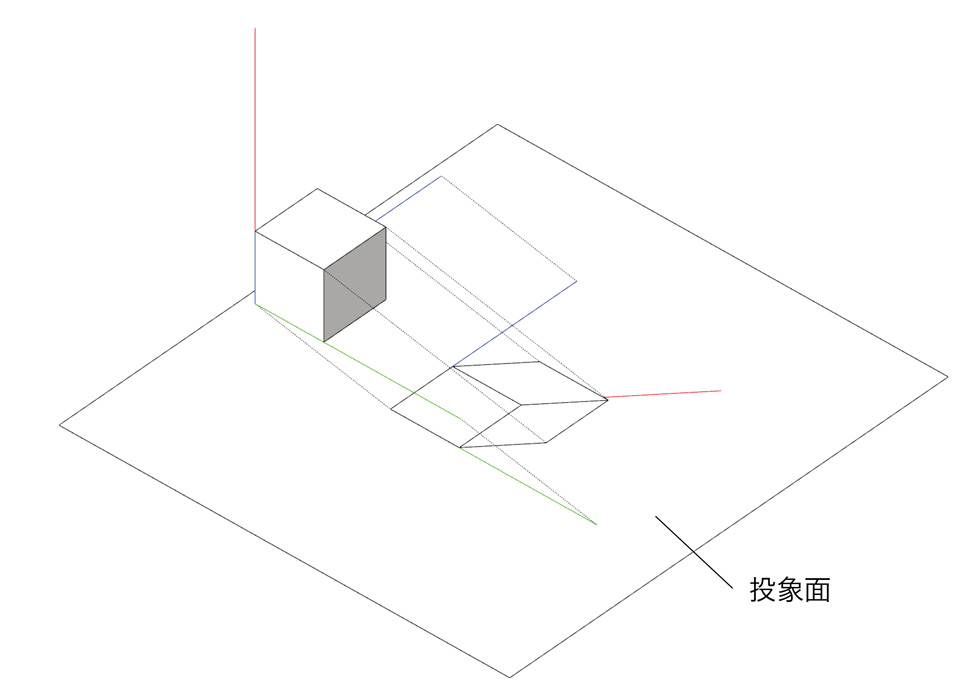
【斜投象の原理】
立体図形の各頂点を通り、投象面に対して垂直ではないR方向に平行な投射線と投象面との交点から立体図形の斜投象が得られる。斜投象においては、主軸面の一つを投象面に平行においても、３軸を一つの投象図にあらわすことができる。このとき、投象面に平行においた主軸面は実形が投象面に現れることが斜投象の特徴である。

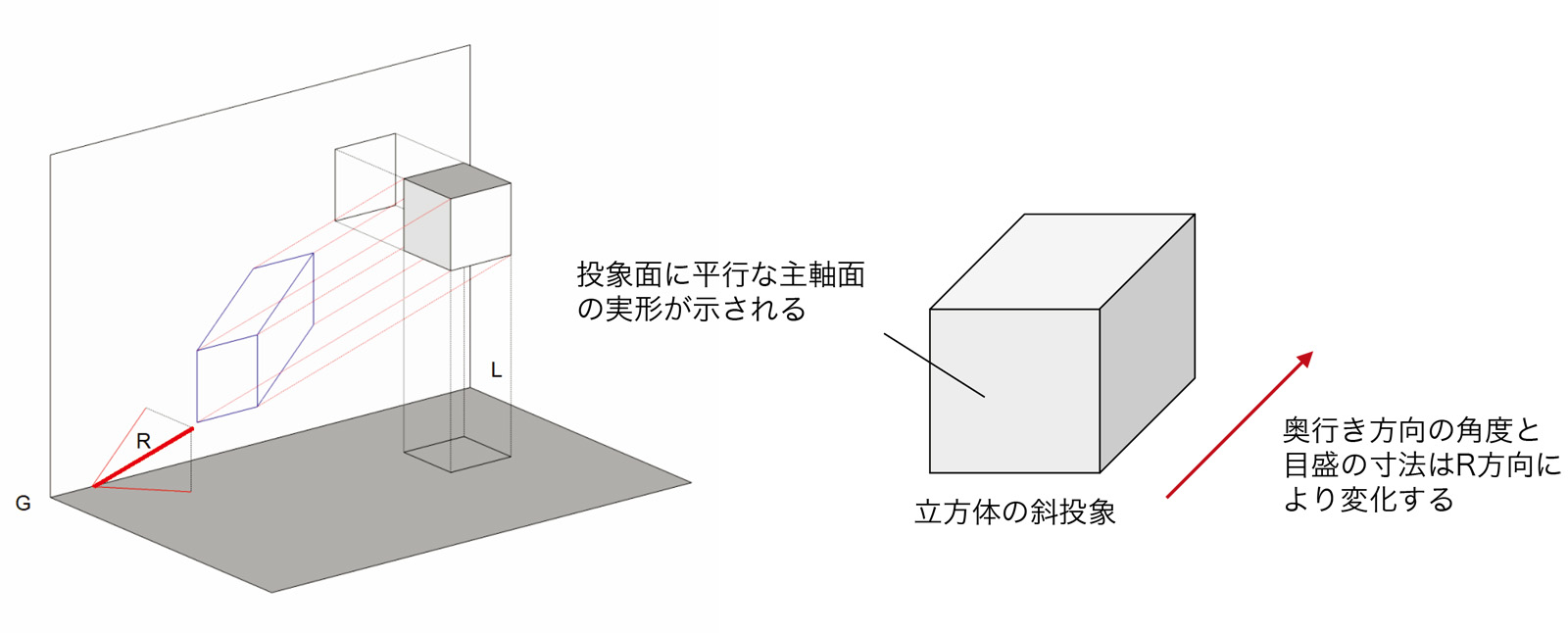
【カバリエ投象】
直立面の2軸を投象面と平行にした斜投象を「カバリエ投象」という（騎兵が馬に乗って事物を眺めた時に見えるような図が得られるところからカバリエ投象という）。カバリエ投象は、直立面と平行な面に実形が示されるため、直立面の形状の表示に主眼を置く場合によく用いられる（下図参照）。

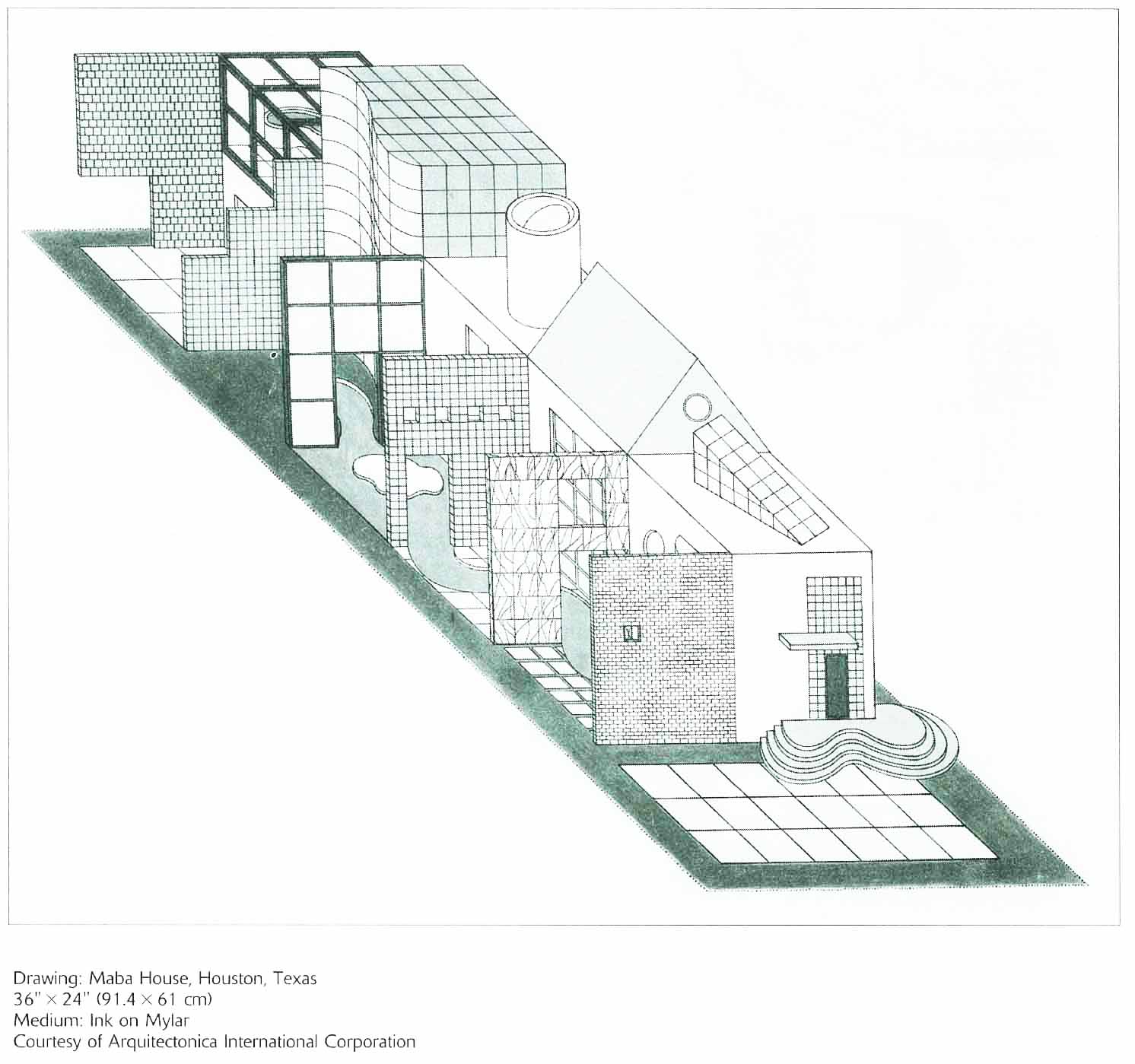
【ミリタリ投象】
水平面の2軸を投象面と平行にした斜投象を「ミリタリ投象」という（陸軍で要塞の図によく使用されたりしたところからミリタリ投象という）。ミリタリ投象は、水平面と平行な面に実形が示されるため、水平面の形状の表示に主眼を置く場合によく用いられる（下図参照）。

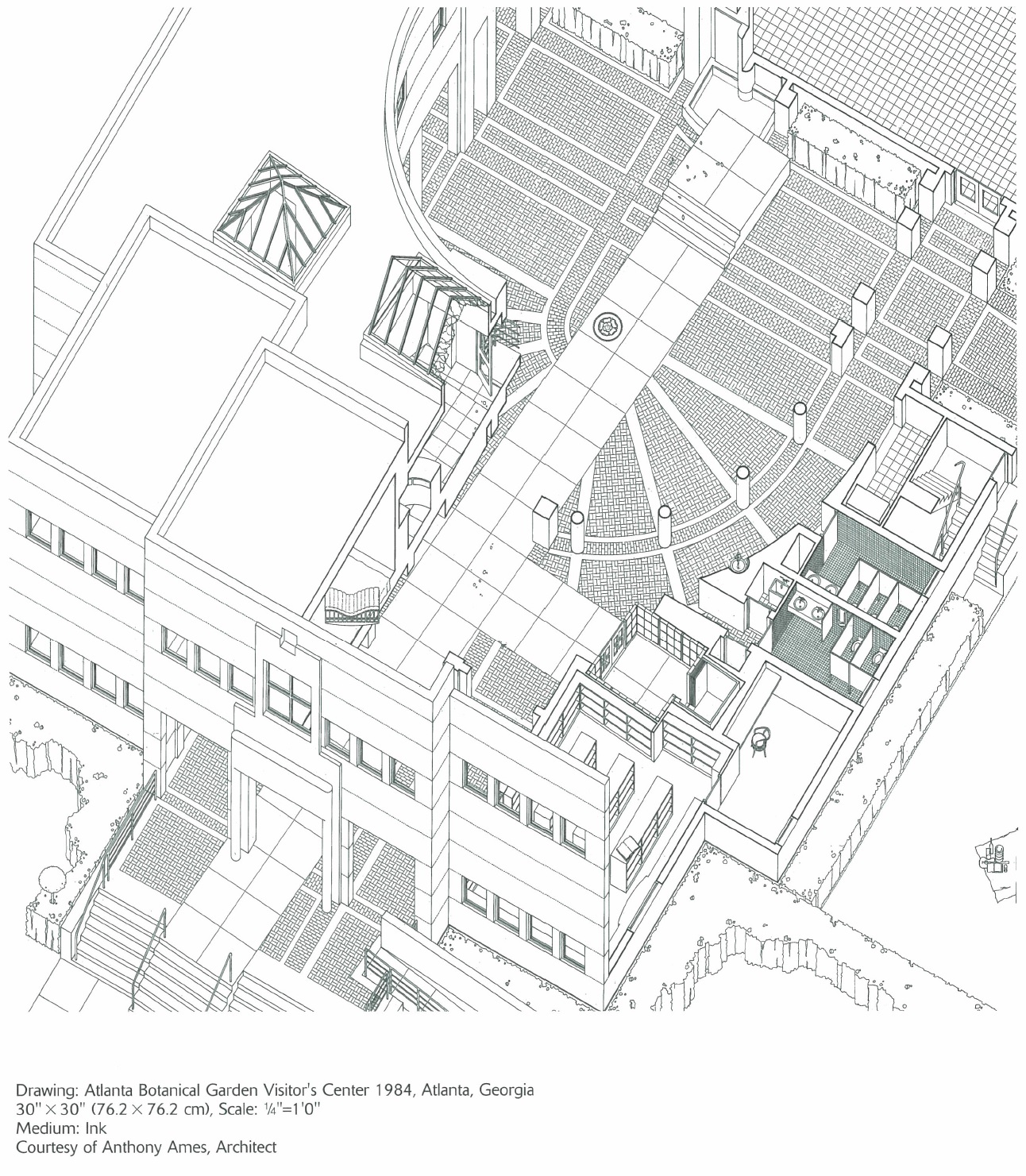
【斜軸測比と斜軸測角】
3軸の手前方向をX軸、右方向をY軸、上方向をZ軸としたとき、カベリエ投象の場合はYZ軸に平行な面に実形が現れ、奥行き方向となるＸ軸を斜め方向にとる。このときX軸とY軸のなす角を「斜軸測角δ」と呼ぶ。また、X軸の目盛寸法と実寸法の比率を「斜軸測比μ」という。一方、ミリタリ投象の場合は、XY軸に平行な面に実形が現れ、高さ方向となるZ軸を斜め方向にとる。Z軸とY軸のなす角を「斜軸測角δ」、Z軸の目盛寸法と実寸法の比率を「斜軸測比μ」という。ミリタリ投象の場合は、XYZ軸の狭角を保ったままZ軸を垂直方向にとる場合もある。

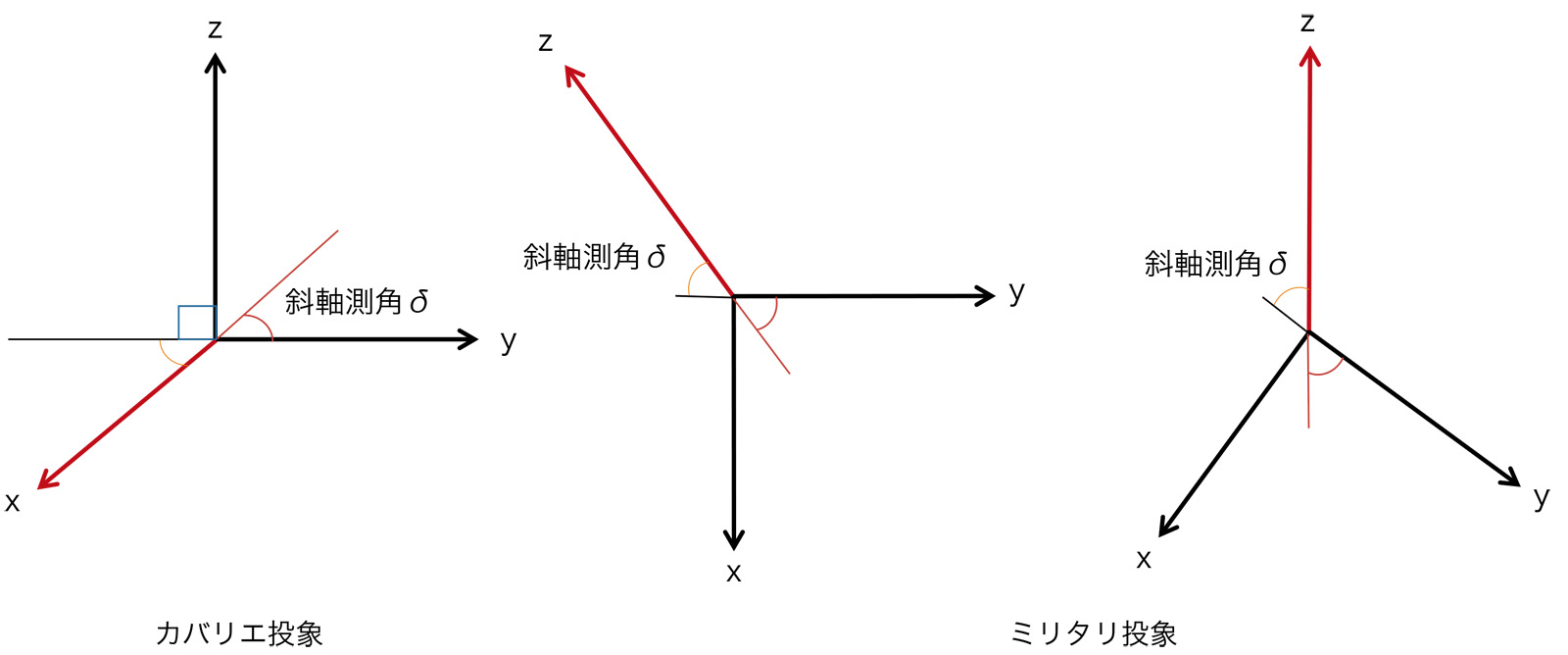
【斜投象の作図】
実用的な斜投象の作図では、まず直交3軸を作図してその3軸を目安に、実形が現れる面から作図する。次にカバリエ投象の場合はX軸方向の長さを、ミリタリ投象の場合はZ軸方向の長さをμの比率にとり、それぞれの斜投象を描く。曲線や曲面は、それを包括する矩形や直方体の斜投象を描き、その後曲線や曲面上の点の座標をプロットして雲型定規で結ぶことにより斜投象を求める。斜投象の原理から、投象面に対する投射線の方向によって斜軸測比と斜軸測角は変化する。斜軸測角や斜軸測比を経験的に基づいて決める必要があり、決めないでおくと、描き手毎に異なった図が得られる。

作図題3-1
(1) 一辺5cmの立方体を斜投象(ガバリエ投象、δ=60°μ=1/2)で作図しなさい。
(2) 一辺5cmの立方体を斜投象(ミリタリ投象、δ=45°μ=1)で作図しなさい。
作図データ

参考
注意「カバリエ投象」の定義には諸説あり、本によって定義が異なっているのが実情です。教科書『実用図学』では傾角45度比率１で垂直な投象面に描かれたものをカバリエとしましたが、広義の解釈では角度や比率にこだわらず、直立投象面に描かれた斜投象（つまり立面図を取り込んで描くもの）全体をカバリエと呼んでいる場合もあります。少なくともカバリエが直立面への投象で、ミリタリが水平面への投象という分類で理解してください。上記の作図では広義に解釈してください。

【斜投象の特徴】
斜投象は、一般によく使われているものの、斜交軸を含む面の作図が決定的でないため、正確な形態表現を求められる図を描くのに向かない。また球も楕円となり球に見えないため、球の多い見取り図にも向かない。

3) 軸測投象

軸測投象の中で、投射線が投象面に垂直な場合を「正軸測投象」という。本テキストでは、正軸測投象のことを単に「軸測投象」と呼ぶ。軸測投象では、直交3軸と投象面の位置関係によって、軸測軸（投象された直交3軸、主軸ともいう）の「狭角」と「縮率」が変化する。軸測軸の3軸の狭角と縮率がすべて等しくなる軸測投象のことを「等軸測投象（等測投象）」という。一方、3軸の狭角と縮率が異なる軸測投象を「不等軸測投象」という。特に、軸測軸の2軸の狭角と縮率が等しくなる軸測投象のことを「2軸測投象」、軸測軸の3軸の狭角と縮率が異なる軸測投象のことを「3軸測投象」という。

　　

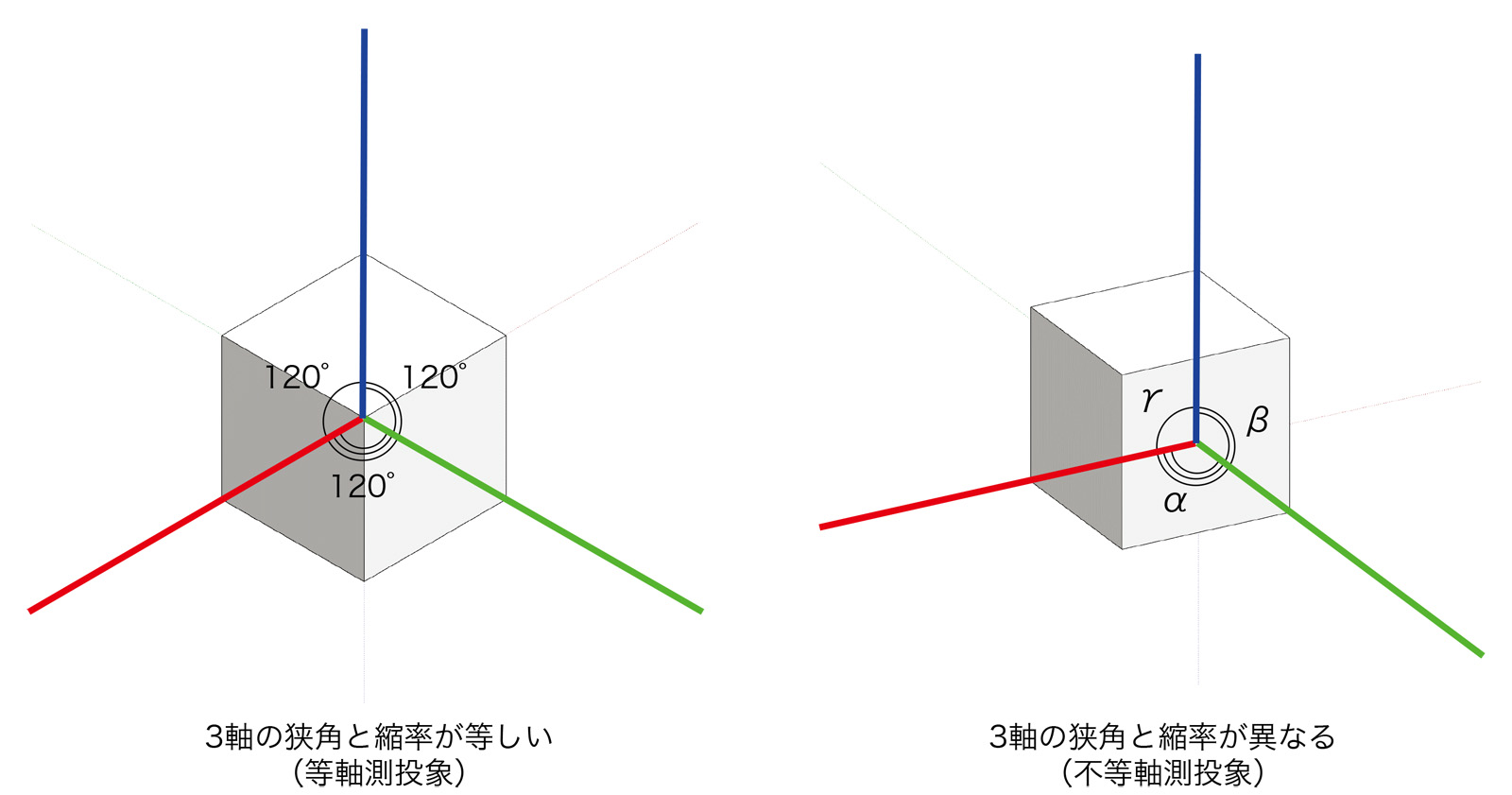
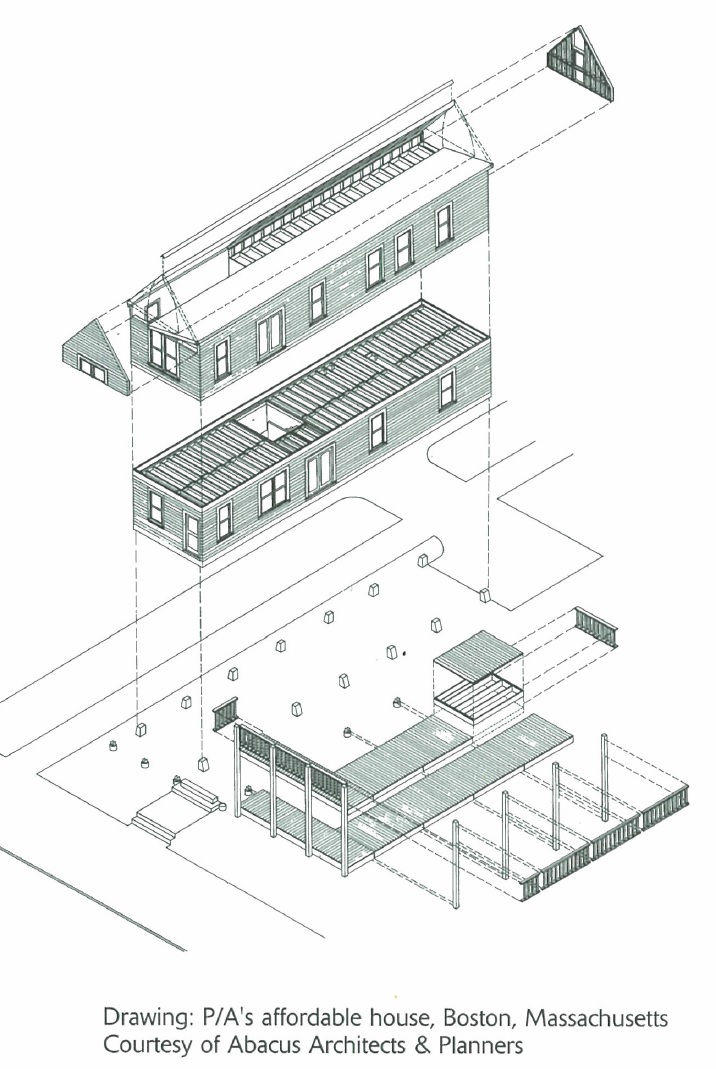
【等軸測投象】/isometric projection
等軸測投象の作図は、まず120°に交わる軸測軸を描き、実長の√2/√3の縮率（理由は後述）で目盛りをとり、その目盛りを手がかりに図を描いていく。このような目盛りを付した軸測軸のことを「軸測尺」という。あらかじめ120°に交わる軸測軸に平行な直線を適当な間隔で引いた用紙は斜眼紙と呼ばれる。√２/√３の寸法間隔で引かれた用紙があれば、等測投象を描くのに便利である。

作図題3-2
下記の正投象から等軸測投象図を作図せよ。

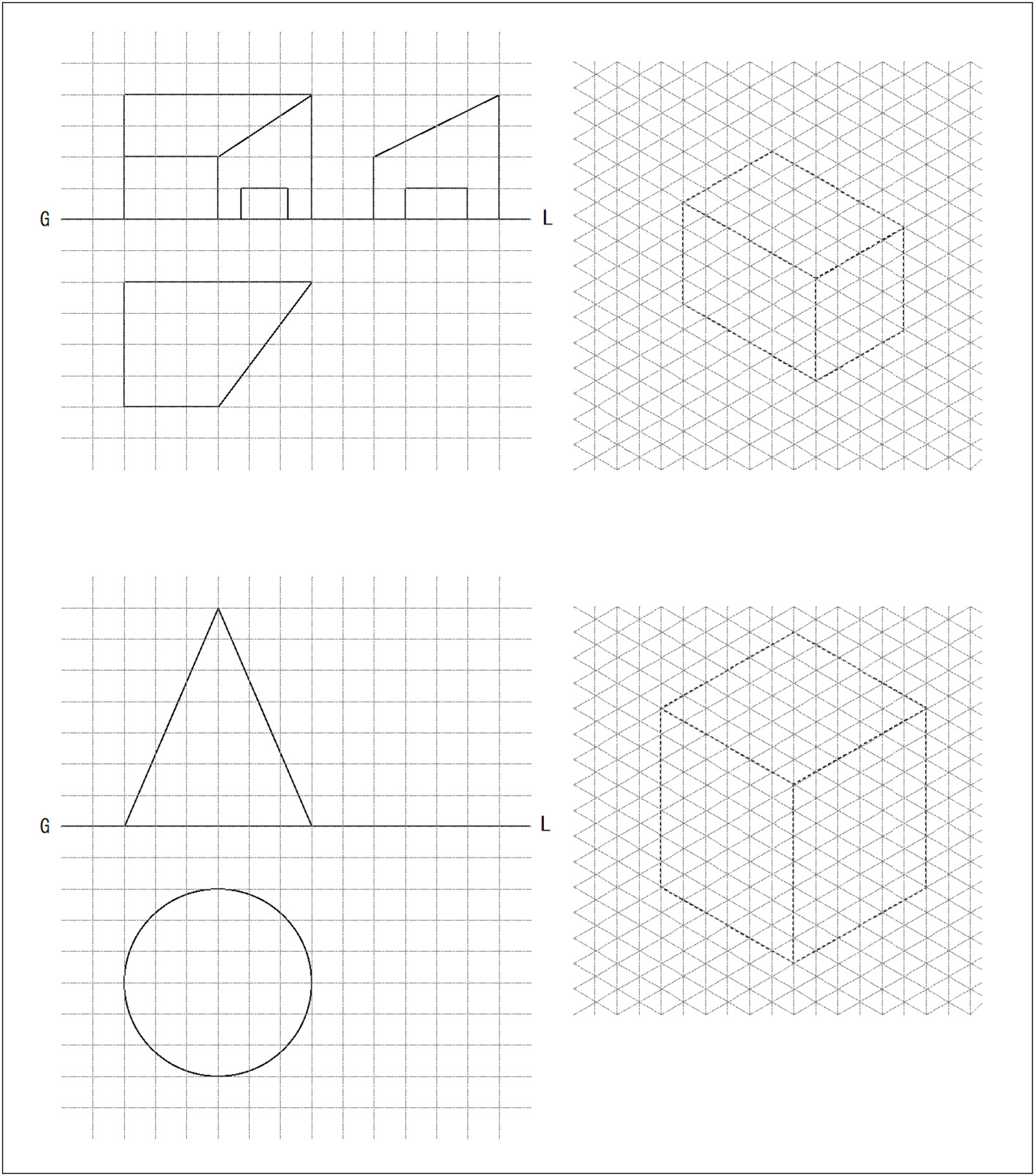
作図データ
参考

等軸図: 市販の斜眼紙は１cmの目盛りになっており、この目盛りに従って図を描くと、現寸よりも大きい図となる。この図は等測図と呼ばれ、等軸測投象と区別することがある。立体形状を提示するための見取り図としては、等測図でも等軸測投象でも正確な形に仕上がっていればよいので市販の斜眼紙を活用してよい。

【不等軸測投象】/axonometric projection
不等軸測投象の作図は、等軸測投象のような斜眼紙を活用できないため、次の手順に示すような軸測尺を作図する必要がある。
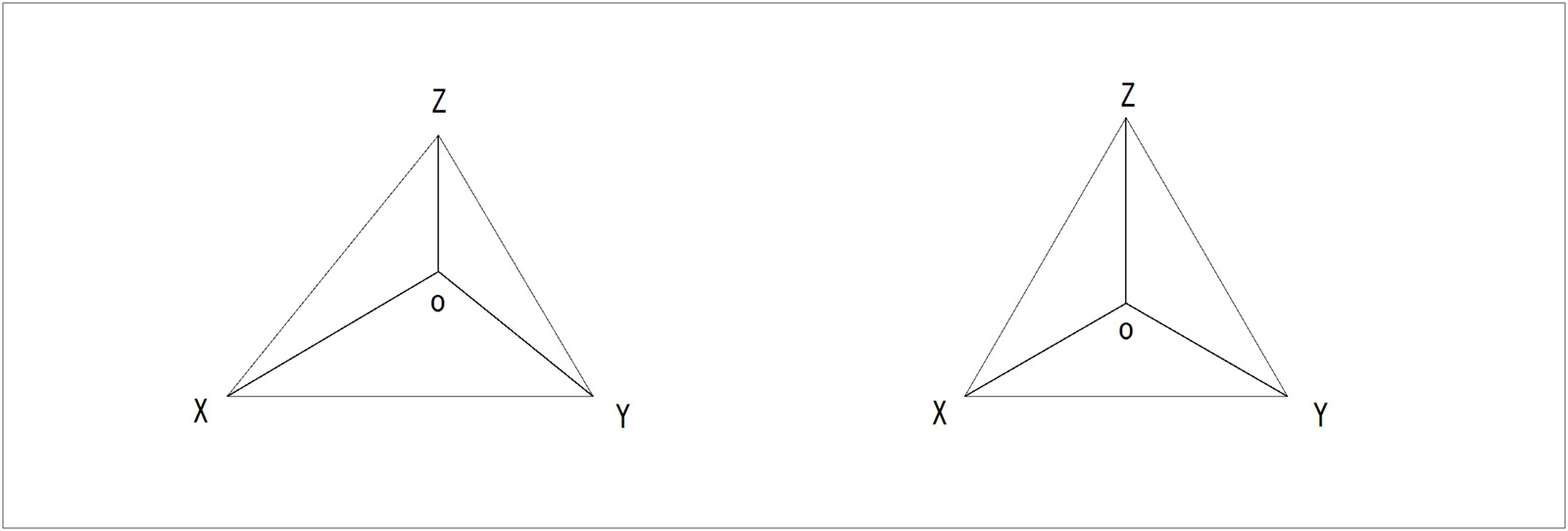
まず、水平面の上空に立方体が斜めに置かれていることを想定する。上から見える3面を延長して投象面との交線（跡）XY, YZ, ZXを求めると、OXYZは三角錐となる。これを平面図として見ると、oX, oY, oZが軸測軸であり、oは三角形XYZの垂心となる。この三角形のことを「跡三角形」と呼ぶ。

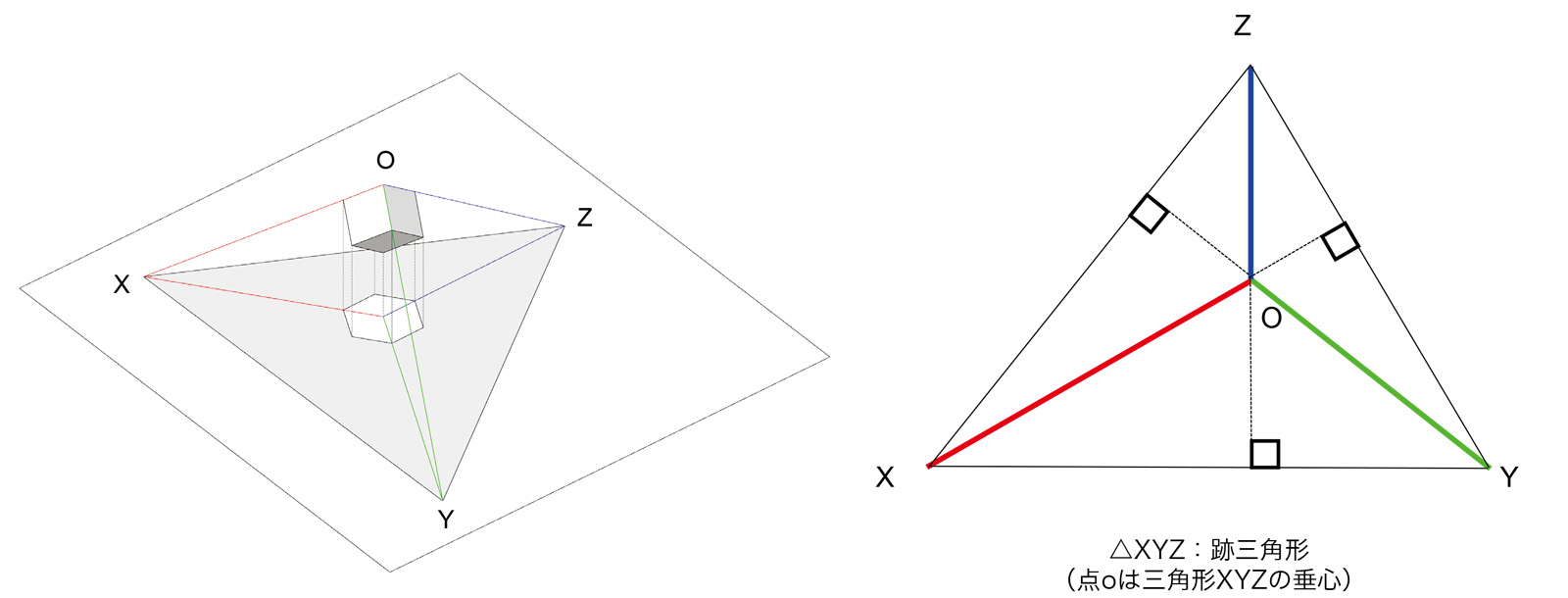
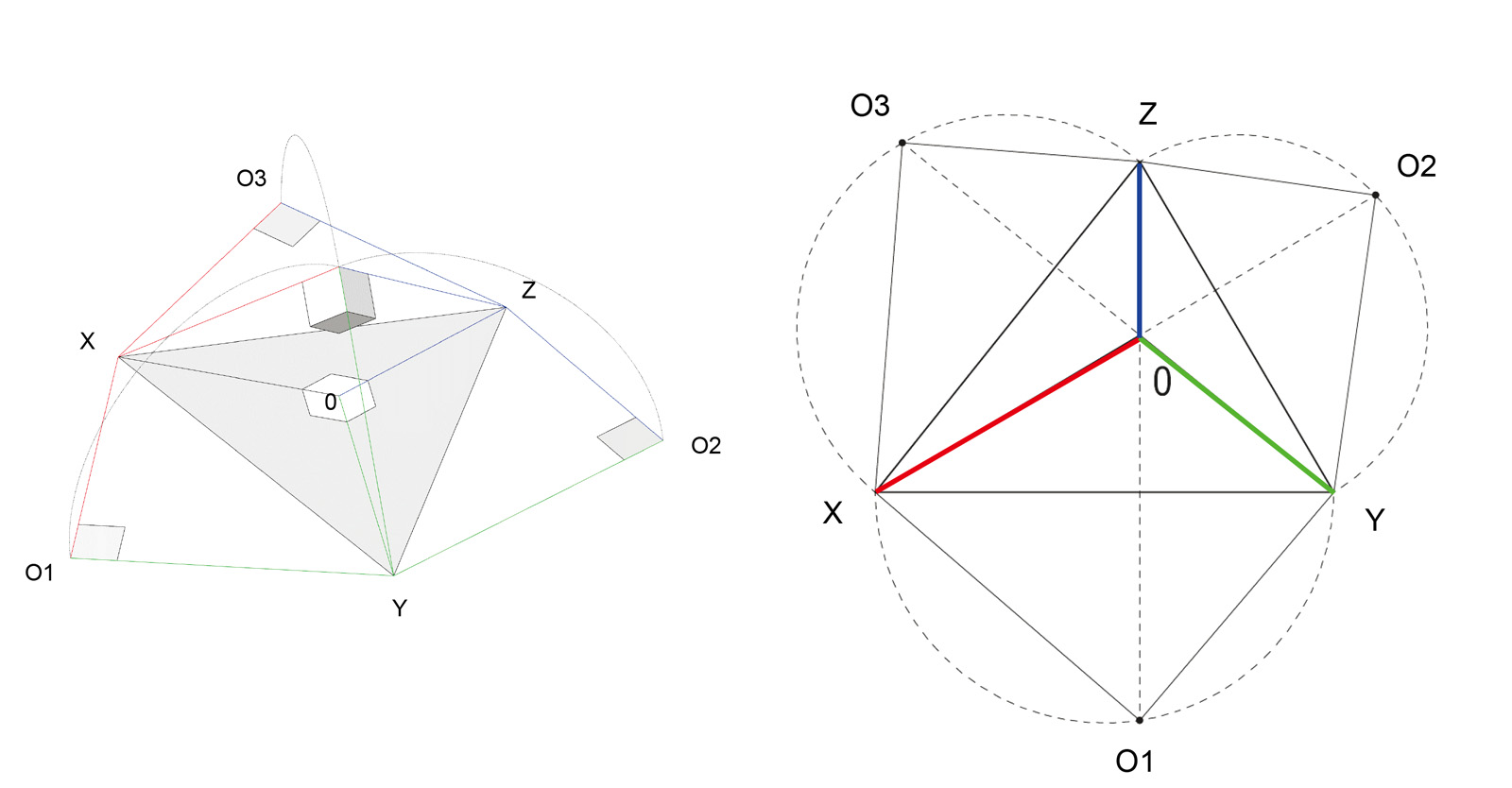
跡XYを回転軸にして、三角形XOYを水平面と重なるまで回転（ラバット）させると、三角形XO1Yとなって水平面上に実形が得られる。このラバットの作図は、三角形XO1Yが直角三角形であることから、XYを直径とする半円とoからXYに下ろした垂線との交点としてO1が求まる。同様にして、三角形YO2Z、三角形ZO3Xを求める。
その結果、X軸の実長はO1X（またはO3X）、Y軸の実長はO1Y（またはO2Y）、Z軸の実長はO2Z（またはO3Z）に現れるため、それに基づいて軸測尺（目盛りを付した軸測軸）が作図できる。

作図題3-3
OX、OY、OZの３主軸を用いて一辺１ｃｍの立方体の軸測投象を描け。

作図データ
参考

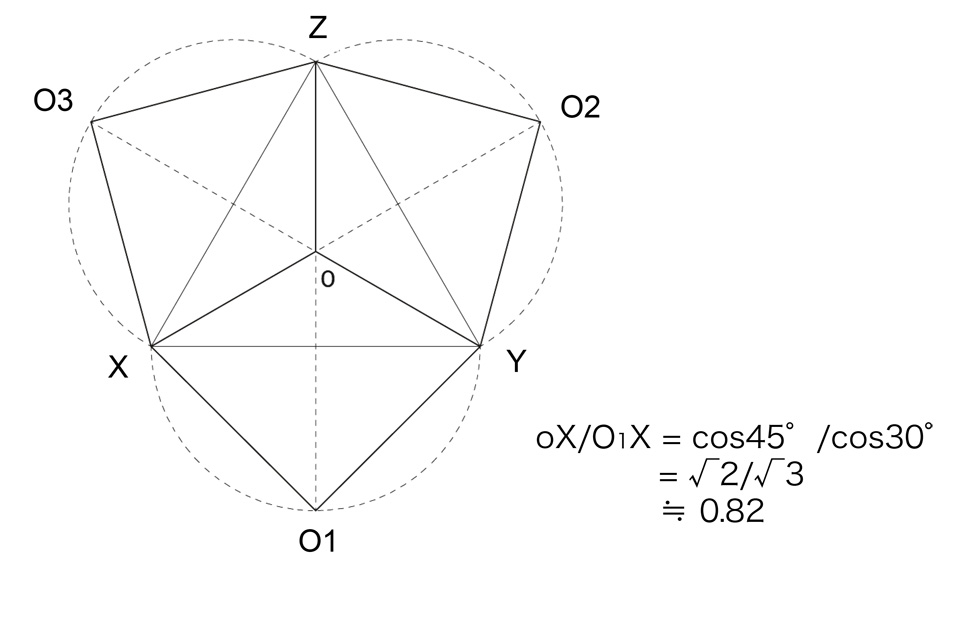
下図から等軸測投象の軸測尺は、O1X, O1Y, O2ZとoX, oY, oZの縮比は√2/√3になっていることが分かる。

作図題3-4
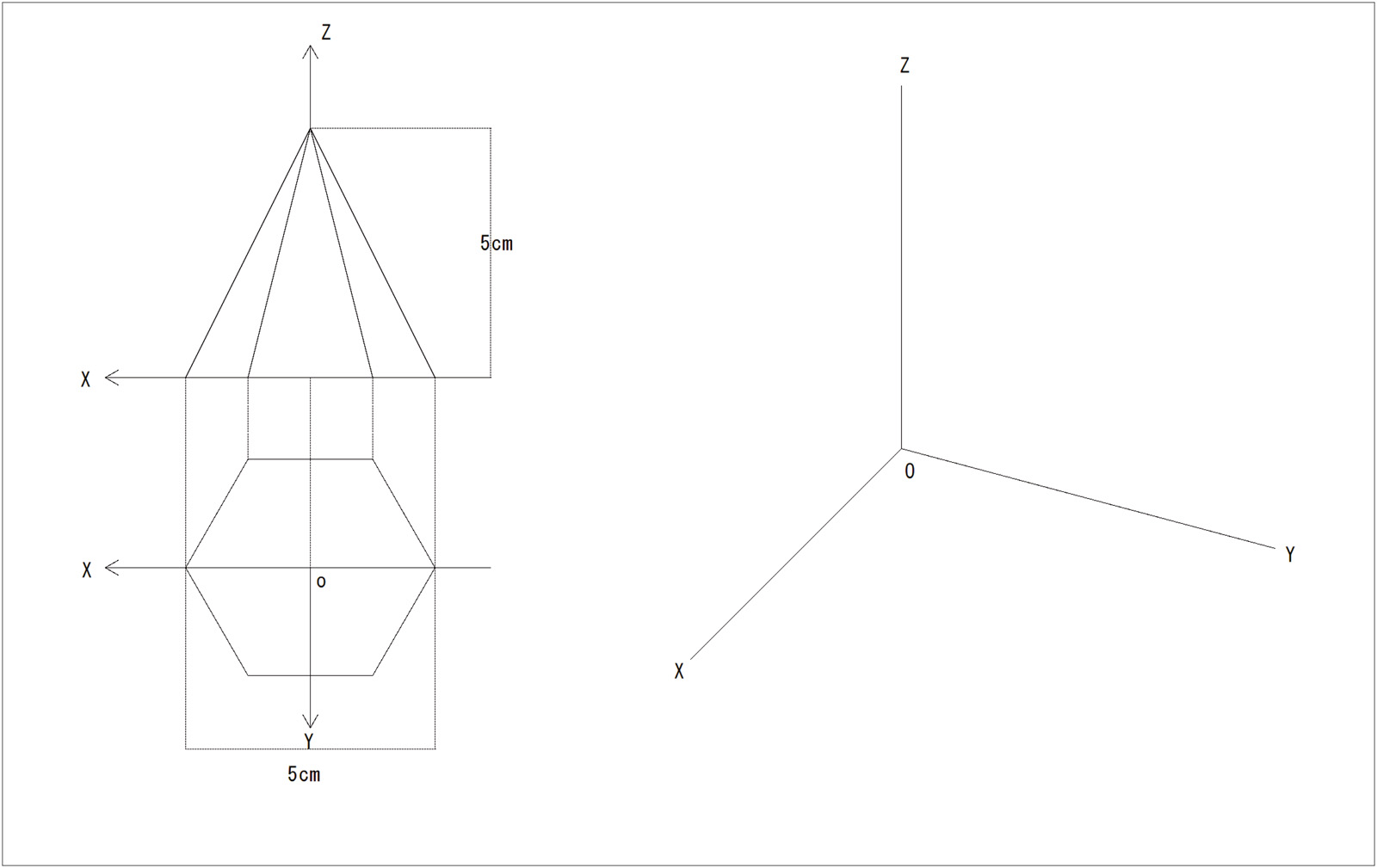
下記の左に示す正投象から右に示すOX、OY、OZを３主軸とした軸測投象を作図せよ。

作図データ
参考

作図題3-5
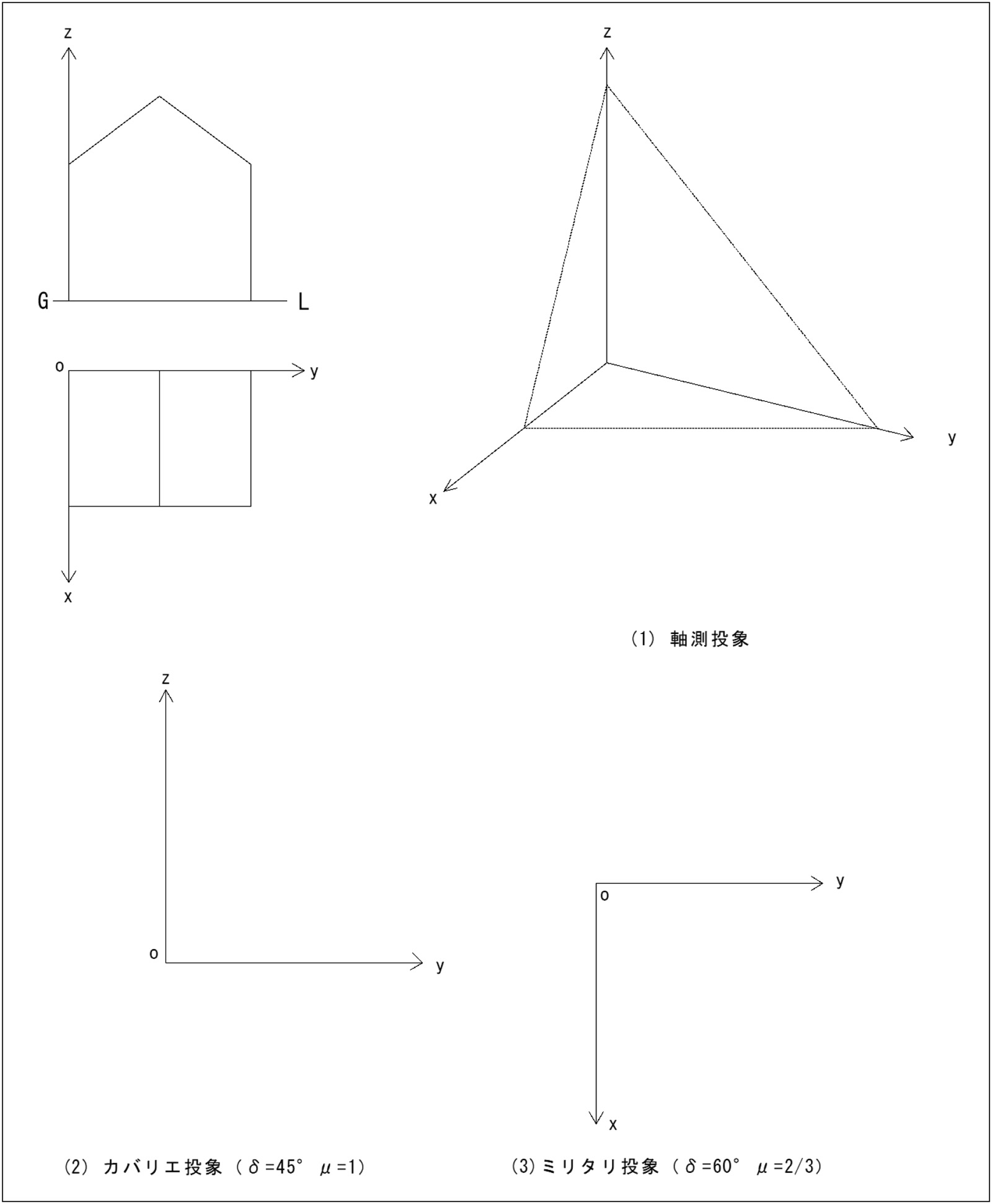
次の正投象で描かれた立体の軸測投象(1)および斜投象(2)(3)を作図しなさい。

作図データ
参考

4) 標高投象/indexed projection
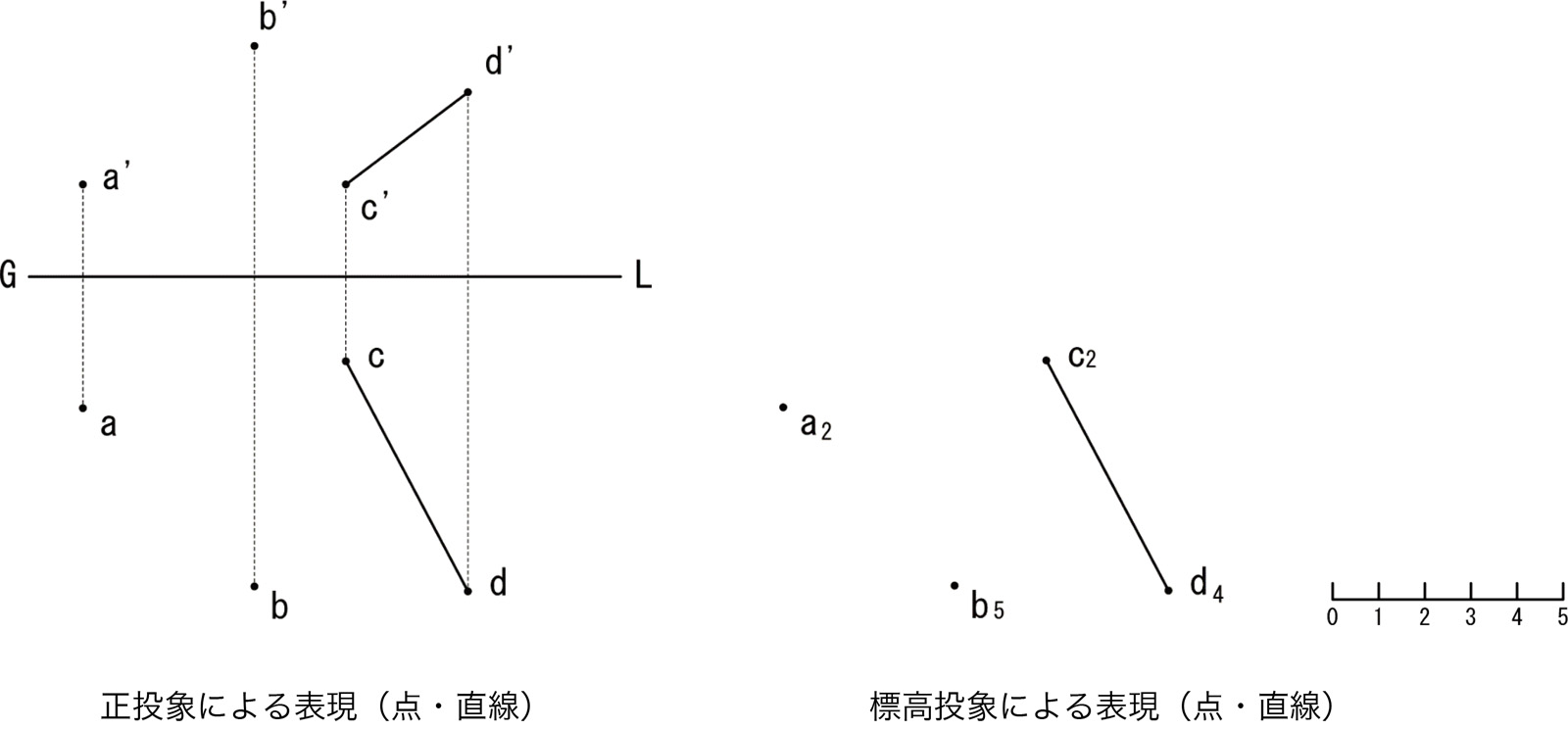
標高投象は、平面図と基準面からの高さ（標高）により立体空間を描く図法である。正投象では高さを立面図によってあらわすが、標高投象は立面図を描かないで、標高を平面図の記号に付記して、立体を平面図のみであらわす単面投象である。

【等高線と勾配尺】
平面の等高線（等高線は平行）に垂直に交わる直線上に等高線の目盛りを写して数値を記入し、さらに太い平行線を左右どちらかに引いた図を平面の勾配尺と呼ぶ。勾配尺は平面の最大傾斜方向を示す。

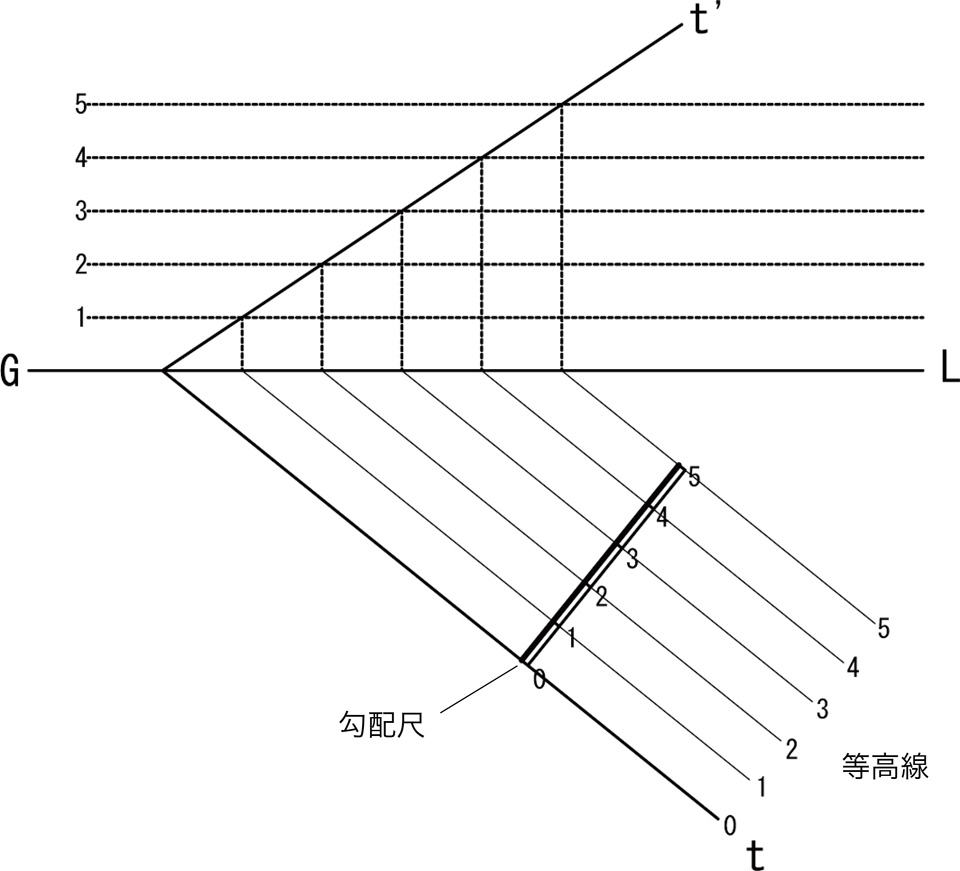
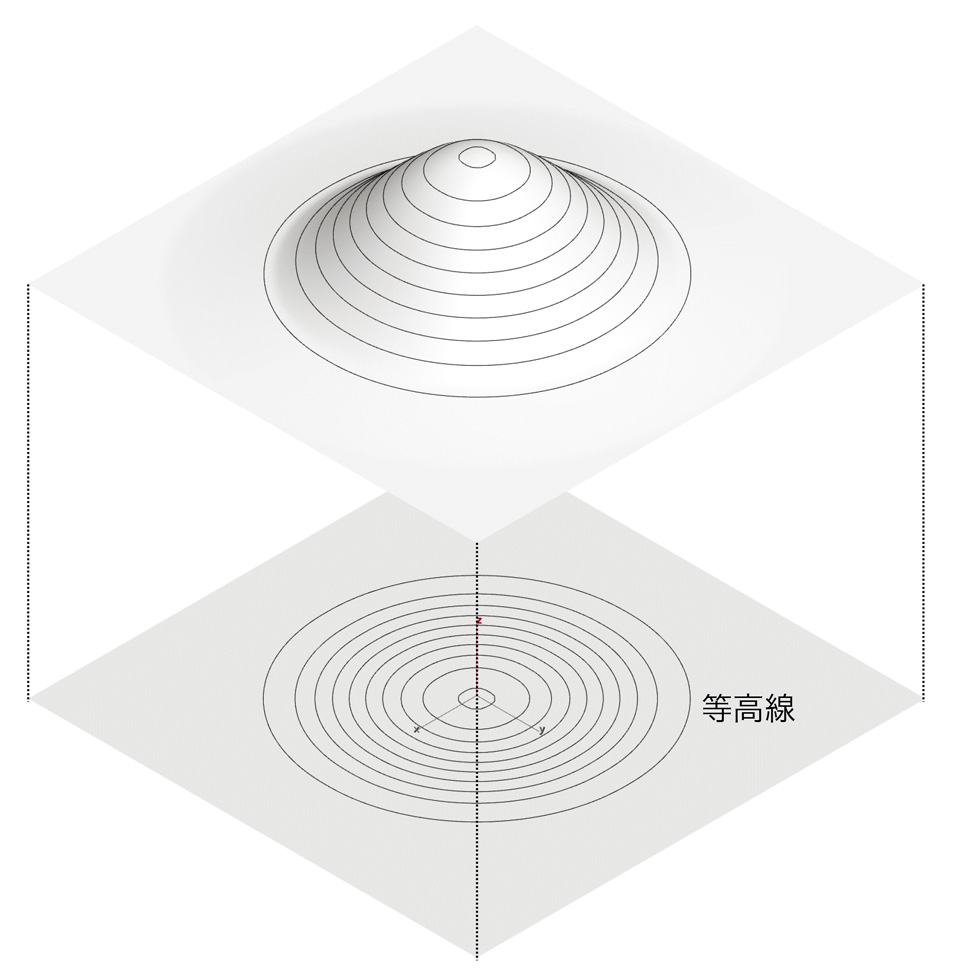
標高の等しい点を結んだ「等高線（contor line）」を描くことで、不規則な高低を持つ地形などを表現するのによく用いられる。

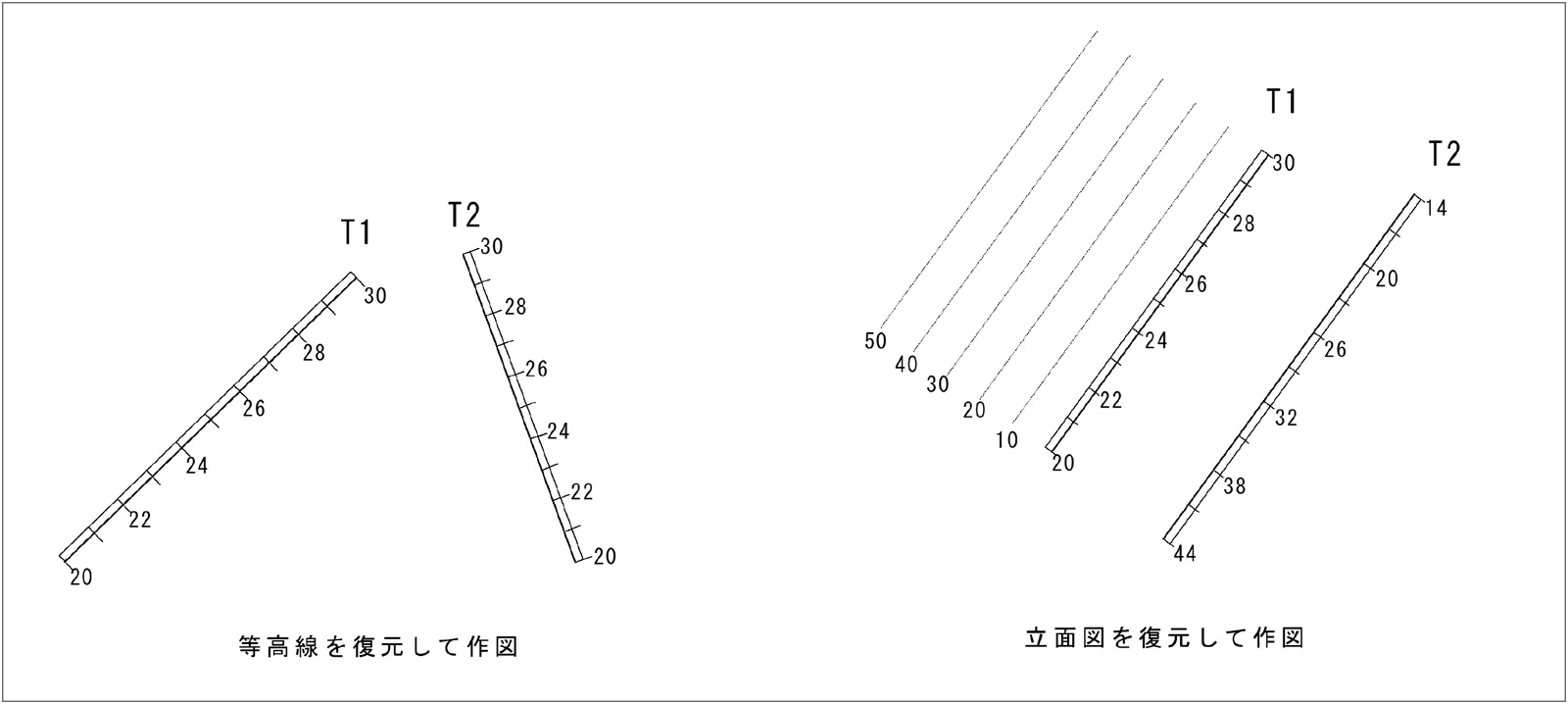
作図題3-6
平面T1, T2の交線を求めよ。

作図データ
参考

作図題3-7
山のふもとの点Aから頂点に向かって1/2勾配の道を山の斜面に沿ってつけよ。

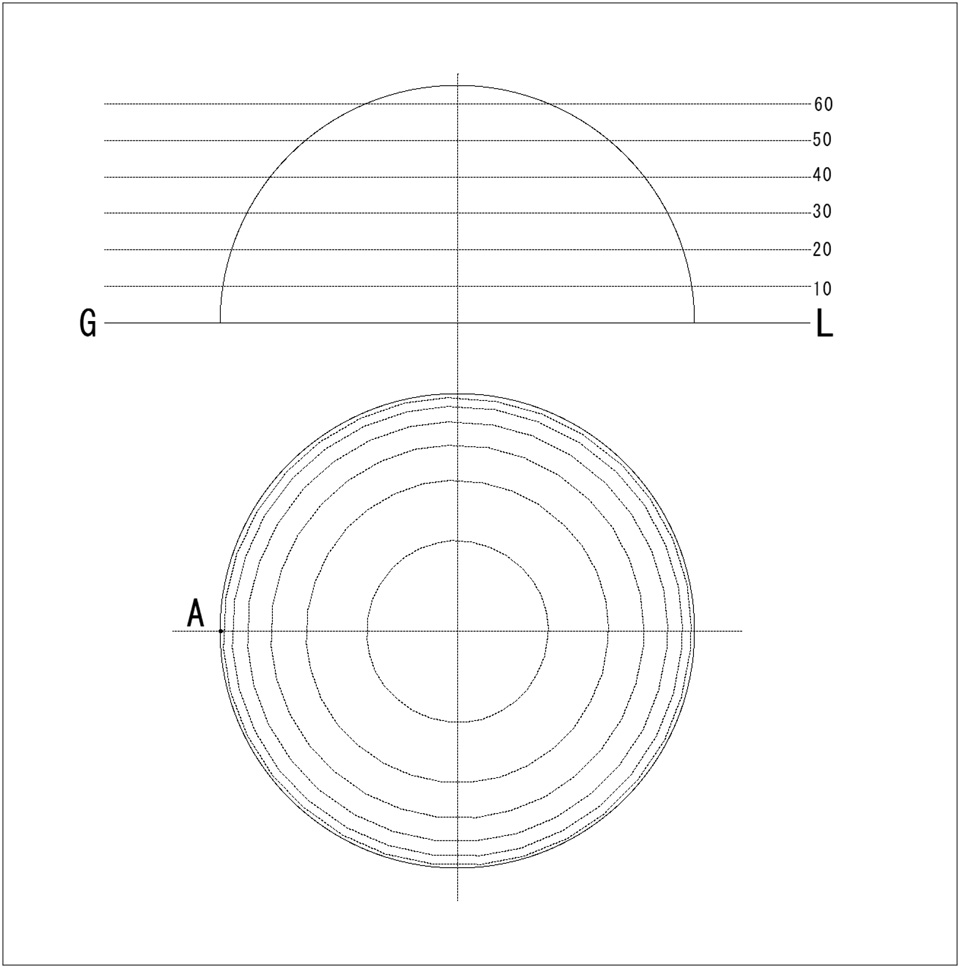
作図データ
参考

作図題3-8
下図のような斜面に高さ60 mの道路を通すことを考える。切土の勾配は4/3、盛土の勾配は4/5として道路完成後の標高投象を求めよ。

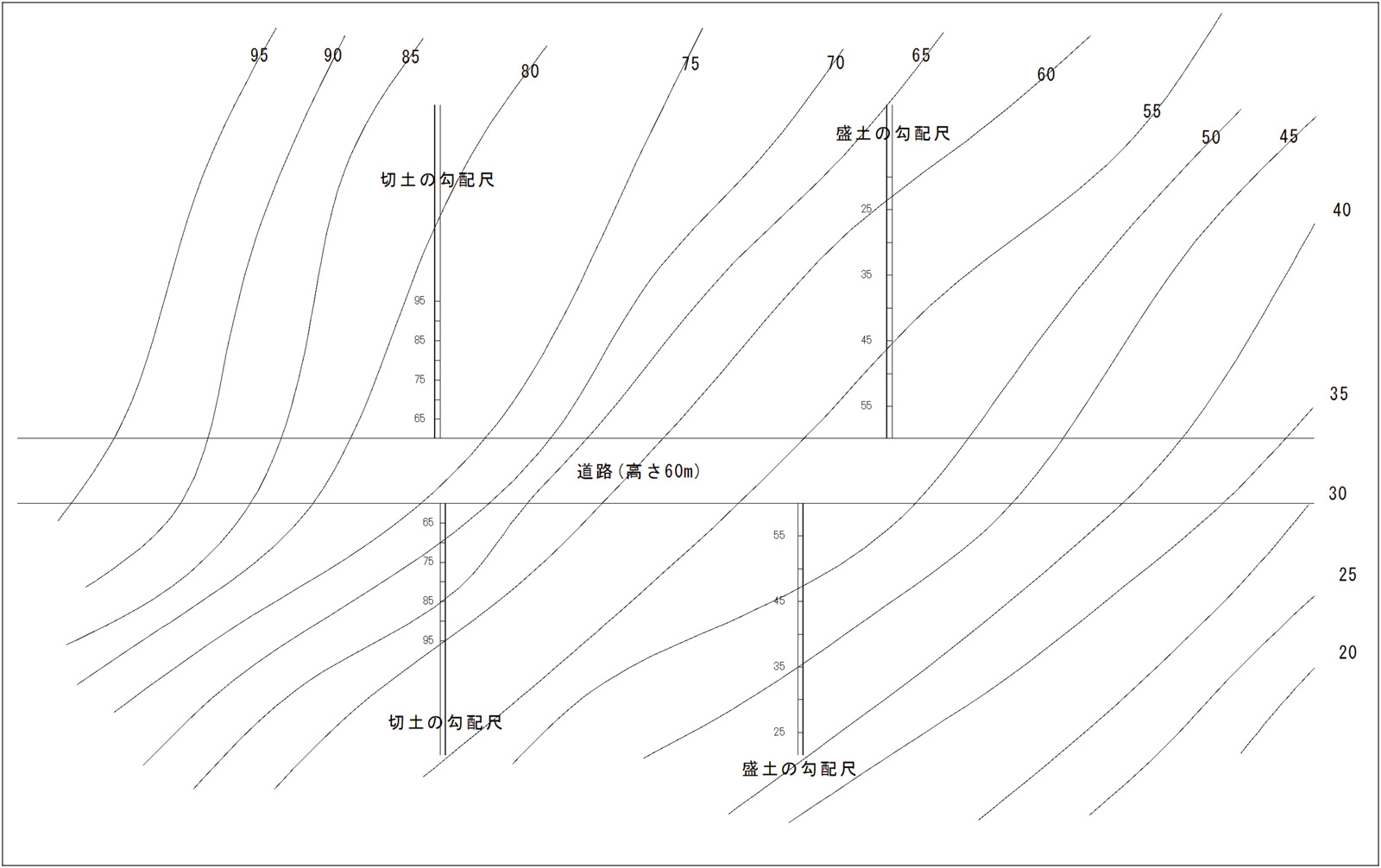
作図データ
参考

5) 透視投象/perspective projection
「透視投象」は、視線（投射線）が一点に集中する「中心投象」である。視線が集中する点を視点と考え、画面（投象面）の向こう側に立体をおくと、視線と画面の交点からなる図（透視図）は人の眼で立体を眺めたものとほぼ同じとなる。

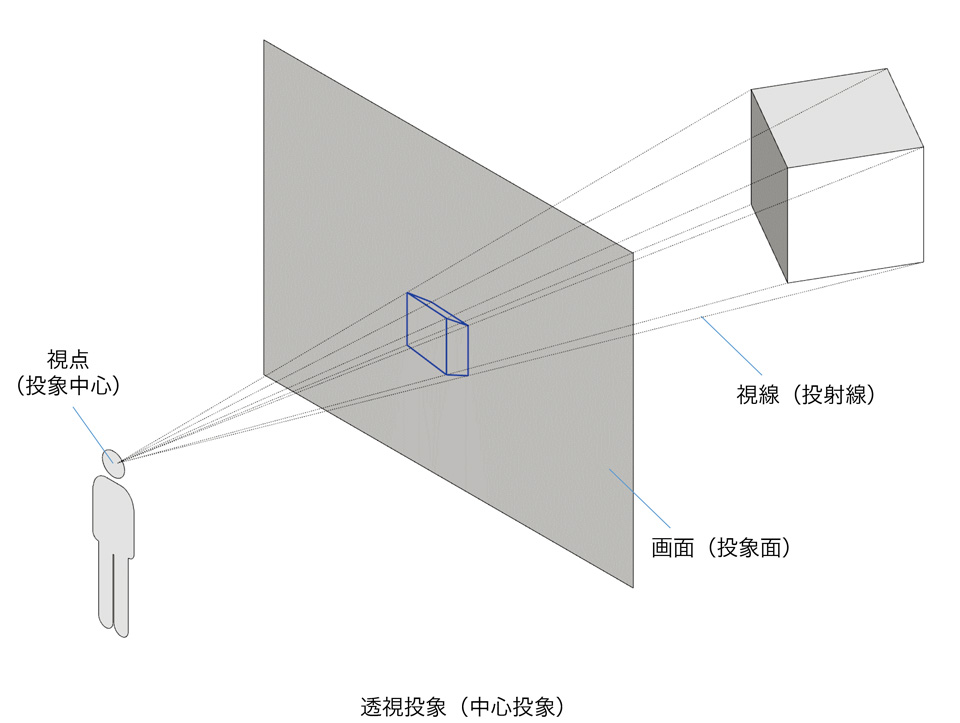
【透視投象の作図（直接法）】
透視図の作図は、視点と画面の位置を設定し、視点から立体を構成する特徴点に伸ばした線（視線）と画面との交点を求めていく。足線（視線の平面図）と目線（視線の立面図）から透視図を作図する方法を「直接法」という。

作図題3-10
点Aおよび点Bの透視投象（A0, B0）を直接法により求めよ。

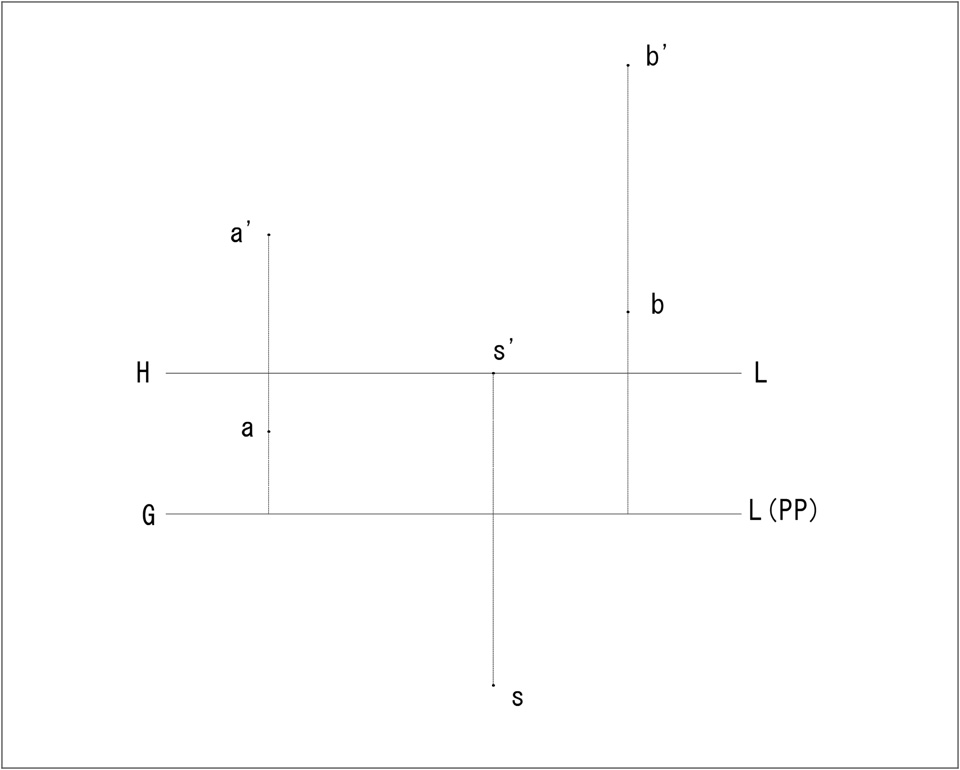
作図データ
参考

作図題3-11
立方体ABCDEFGHの透視投象を直接法により求めよ。

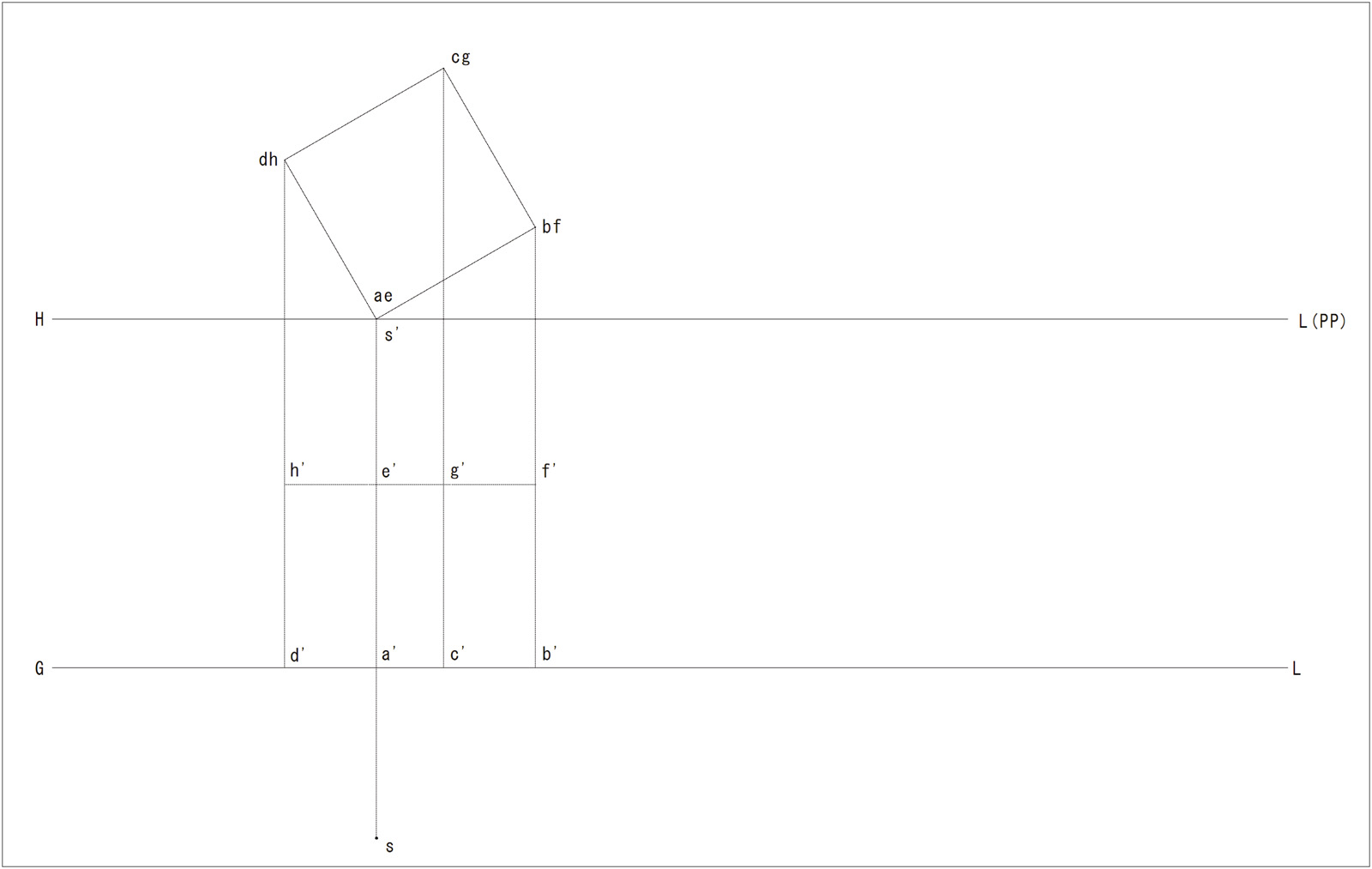
作図データ
参考

【透視投象の作図（消点法）】
直接法は、立体の特徴点を一点一点作図する必要がある。一方、透視投象の「消点（消失点）」を利用することで、平行な線で構成される立体の透視図を効率的に作成することができる（消点法）。
【消点】
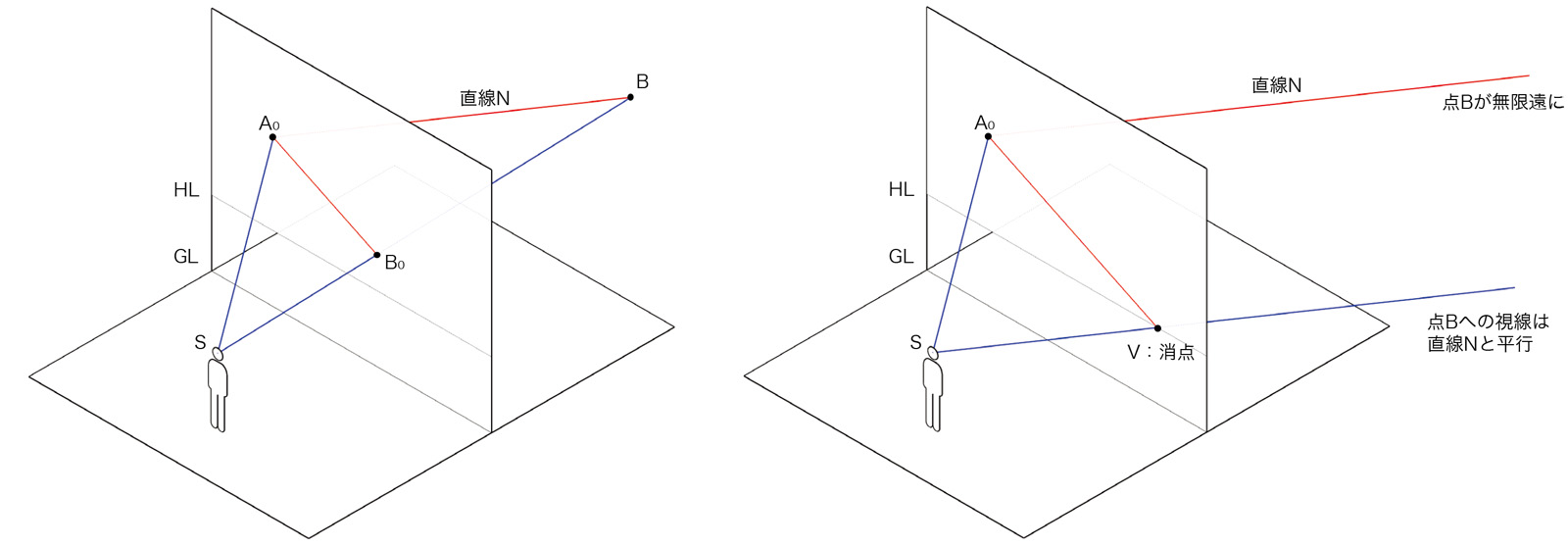
左下図において、(1) 直線Nと画面との交点をA0、(2) 直線N上の任意の点Bと視点Sを結んだ視線が、画面と交わる点をB0とすると、直線A0B0は、直線Nの透視投象を表す。点BがA0から遠ざかると、点B0も視線A0から遠ざかる。それをさらに右下図のように、点Bが画面から遠く離れて無限遠の点になると、点Bと視点Sを結んだ視線が直線Nと平行になる。このとき点Bの透視投象は点Vとなり、この点を直線Nの消点と呼ぶ。

作図題3-13
立方体ABCDEFGHの透視投象を消点法により求めよ。

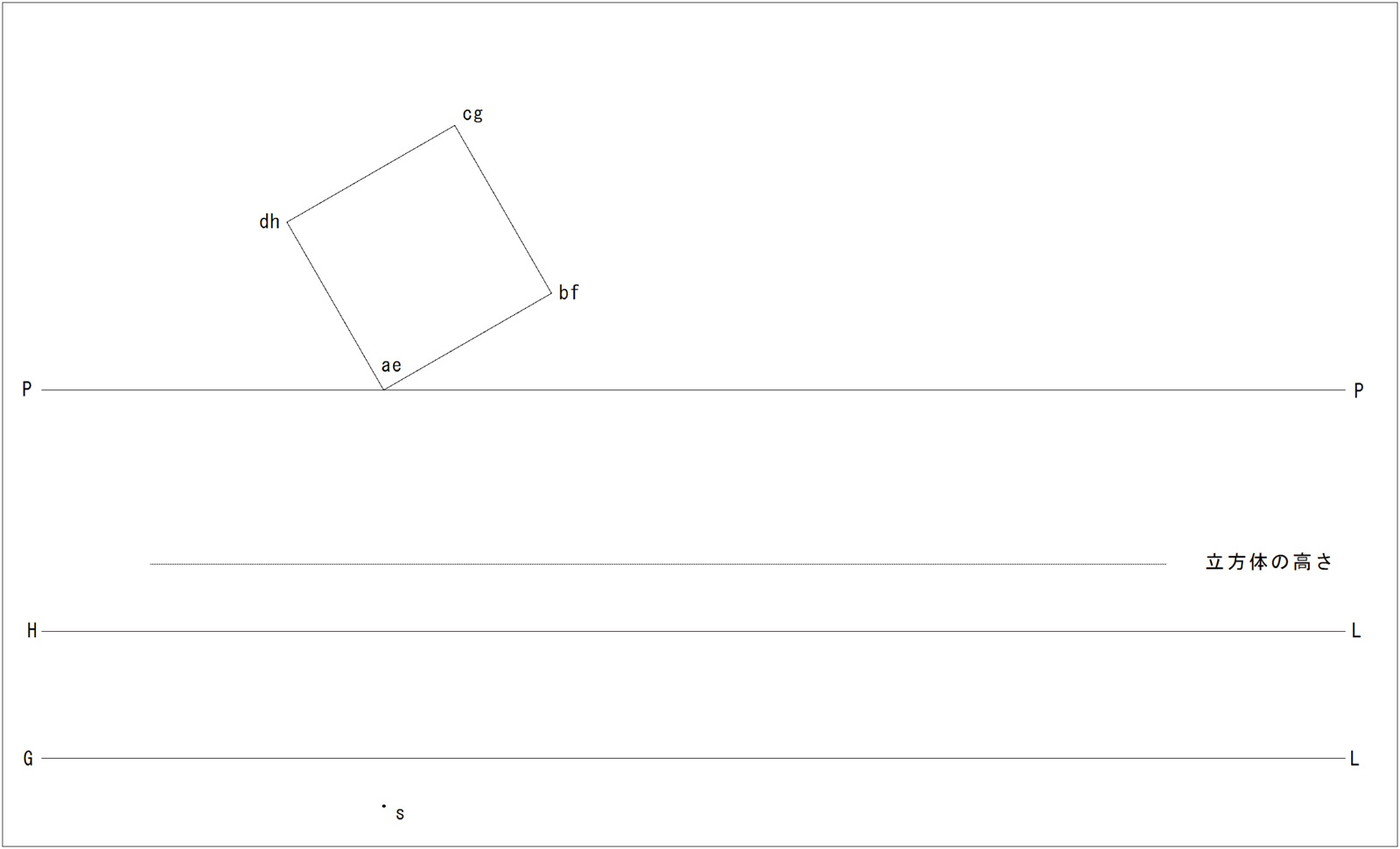
作図データ
参考

作図題3-14

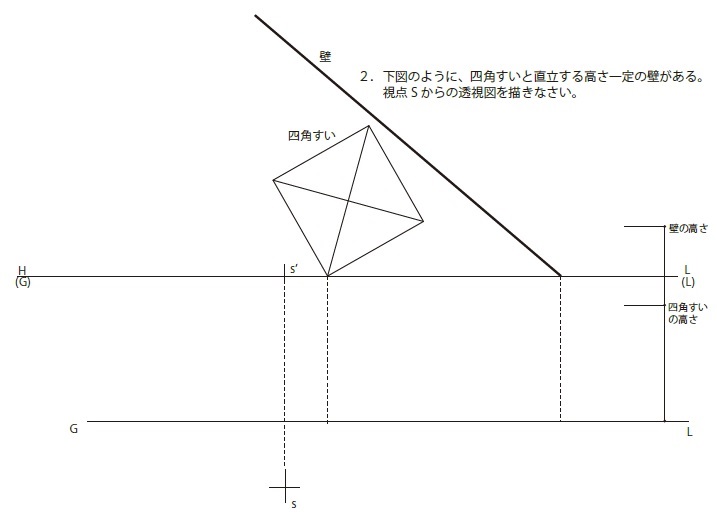
作図データ
参考

作図題3-15

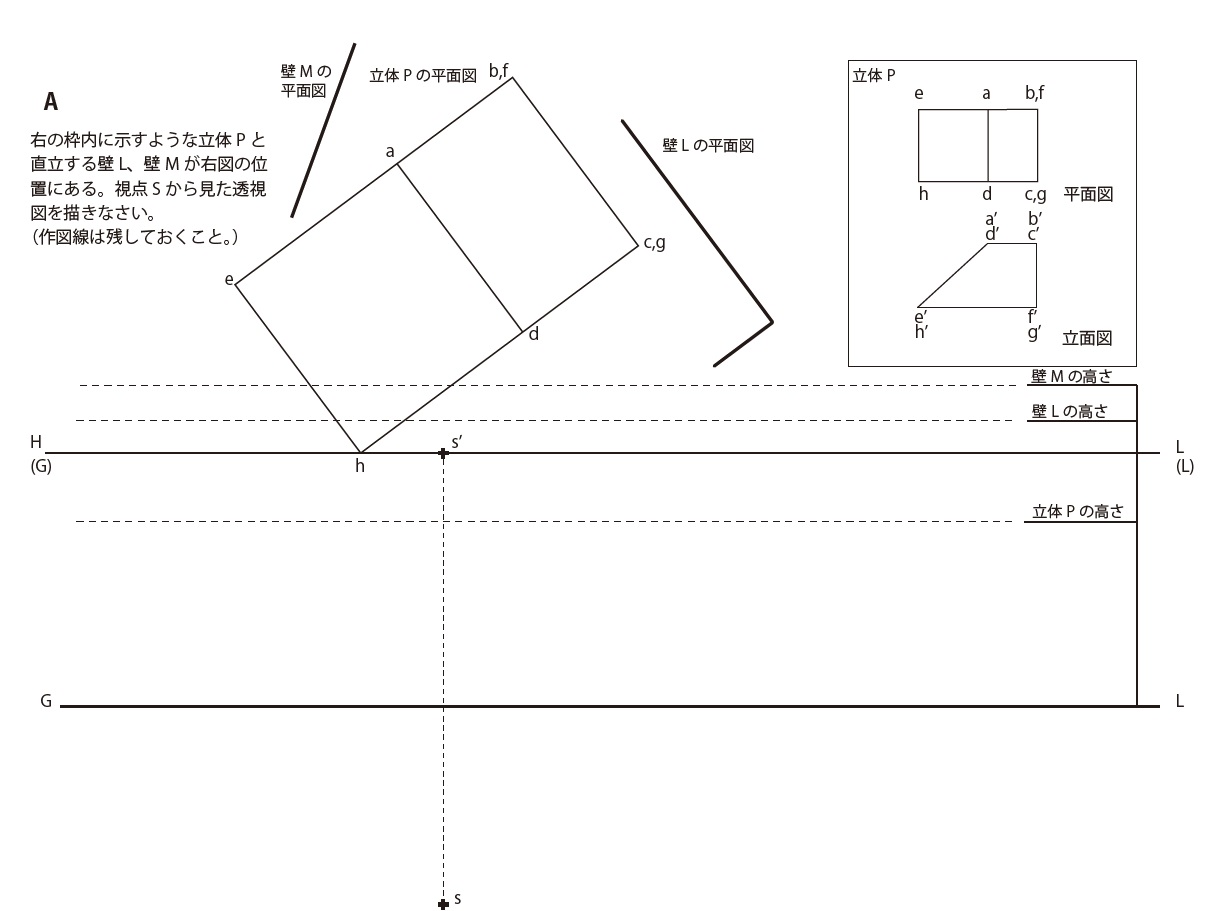
作図データ
参考

作図題3-16

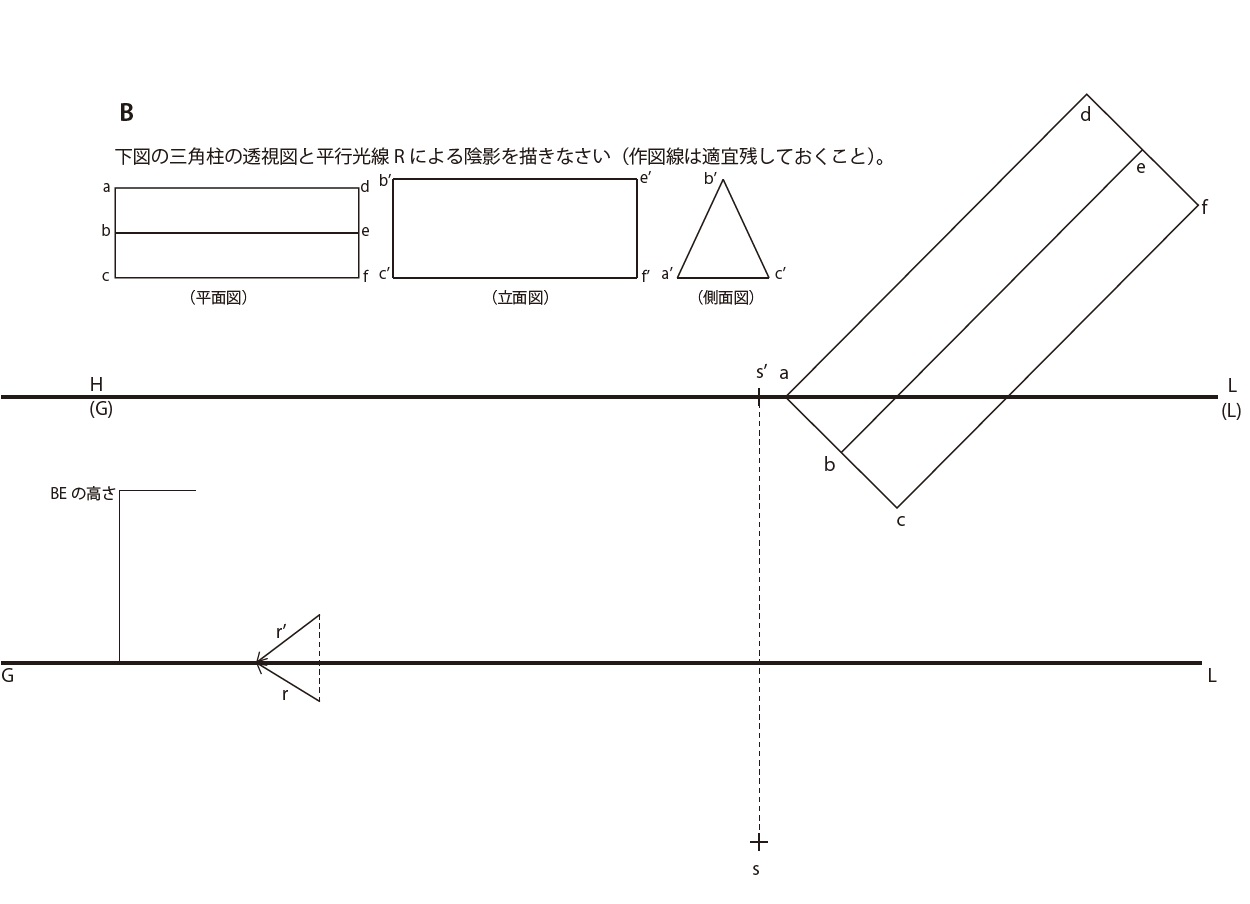
作図データ
参考

第4章　平面から立体へ

空間内の立体の加工・操作によって生じる形状や位置関係を求めるための作図は「図法幾何学」として体系化され，精緻な手書きによって行われてきたが，コンピュータの普及によってその実用性が3D-CAD ツールに置き換わることとなった。しかしながらこのようなツールの根拠となる幾何学的概念についての理解は依然として重要であり，空間認識はより高度な形態的問題を扱ううえでは欠かせない素養である。本章では「図法幾何学」をもとに，立体図形の加工・操作に関わる初歩的な考え方について解説する。

4.1 図法幾何学で用いる投象表現
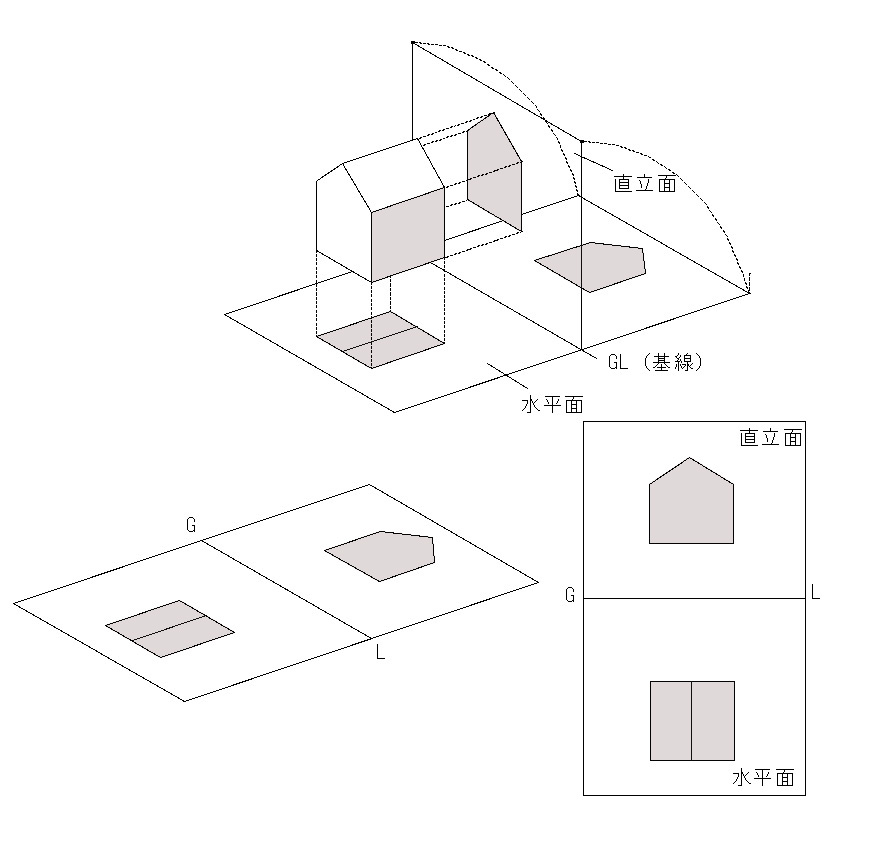
図法幾何学では空間上の2 つの正投象を用いて図形を表現する。ここで水平に置かれた投象面を水平面（HP），垂直に置かれた投象面を直立面（VP），この2 つの投象面の交線を基線（GL）と呼ぶ。また形態要素のそれぞれの投象面への投象を水平投象（または平面図），直立投象（または立面図）という。図法幾何学では図4-1のように，この2 つの投象を基線（GL）を軸に回転させて，図4-2 のように水平に引いた基線の上下に平面図と立面図を配置して作図する。以下ではこの作図法を「複面投象」と呼ぶ。

「複面投象」では空間にある1点の位置を2枚の直角に交わる平面からその点にいたる距離によって示す（図3-1）。ここで水平におかれた平面を水平面（HP）、水平面に直角に交わるもう1つの平面を直立面（VP）と呼び、この2つの平面（主投象面）の交線を基線（GL）と呼ぶ。直交する2つの平面（直立面と水平面）によって区切られた4つの空間（第1象限，第2象限，第3象限，第4象限）内にある1点から直立面と水平面にそれぞれ垂線を引き、その垂線との交点を投象と呼び、それぞれの投象を直立投象（又は立面図）、水平投象（又は平面図）という。この時、空間上の点の実物はアルファベットの大文字（Ａ）を使用し、点の水平面への投象（平面図）はアルファベットの小文字（a）、直立面への投象（立面図）はアルファベットの小文字にダッシュ（a’）をつけて表す。「複面投象」はこの2つの平面（主投象面）の1つを90゜回転させて平面の状態にして表現する。

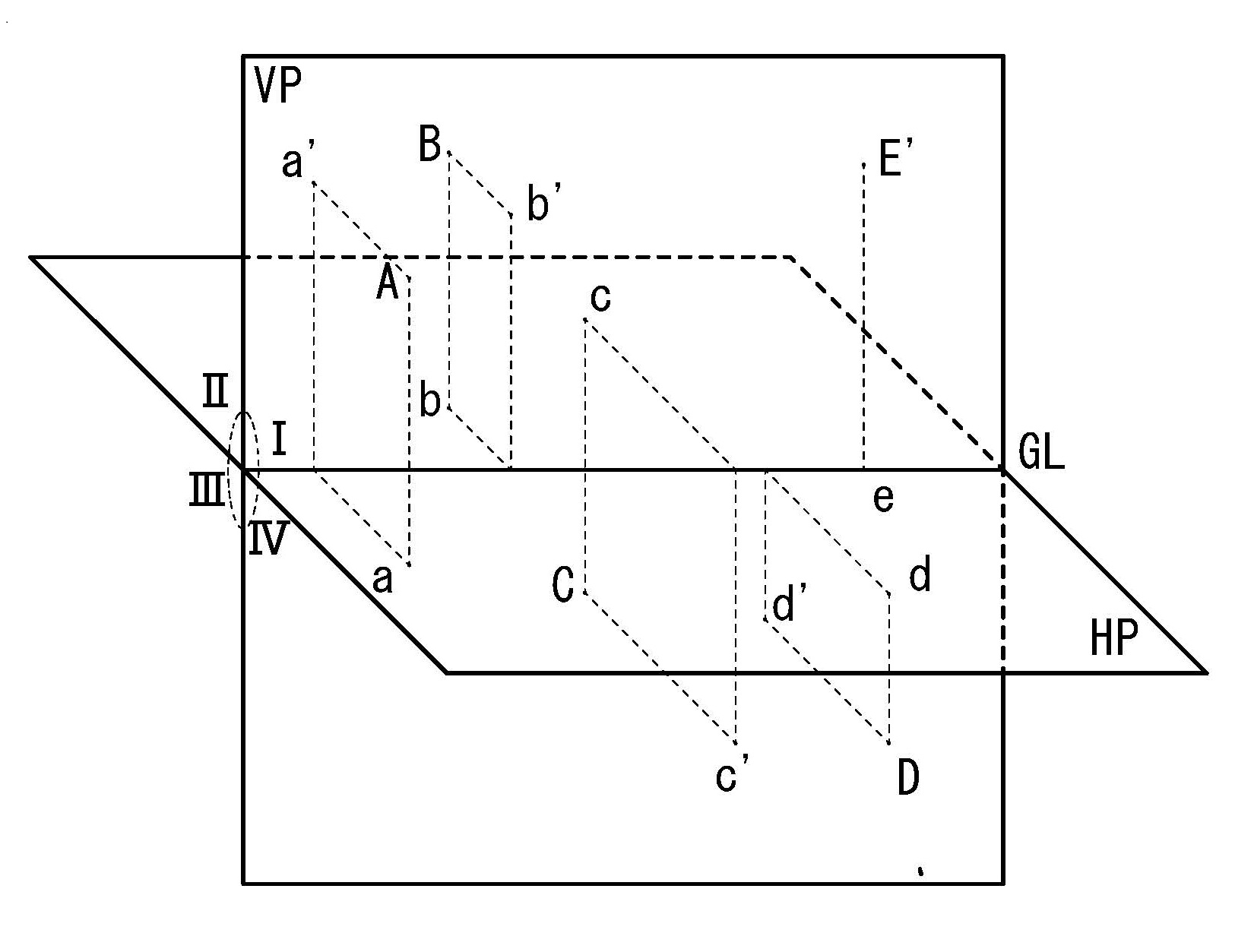
図4-1

【点の表現】
図3-1のように空間上にある点を「複面投象」で作図すると図3-2のように表現され、基線GLより上部が立面図、下部が平面図となる。この時、或る点(A)の立面図(a’)と平面図(a)を結ぶ線を「対応線」と呼び、基線GLに対して常に直交する。

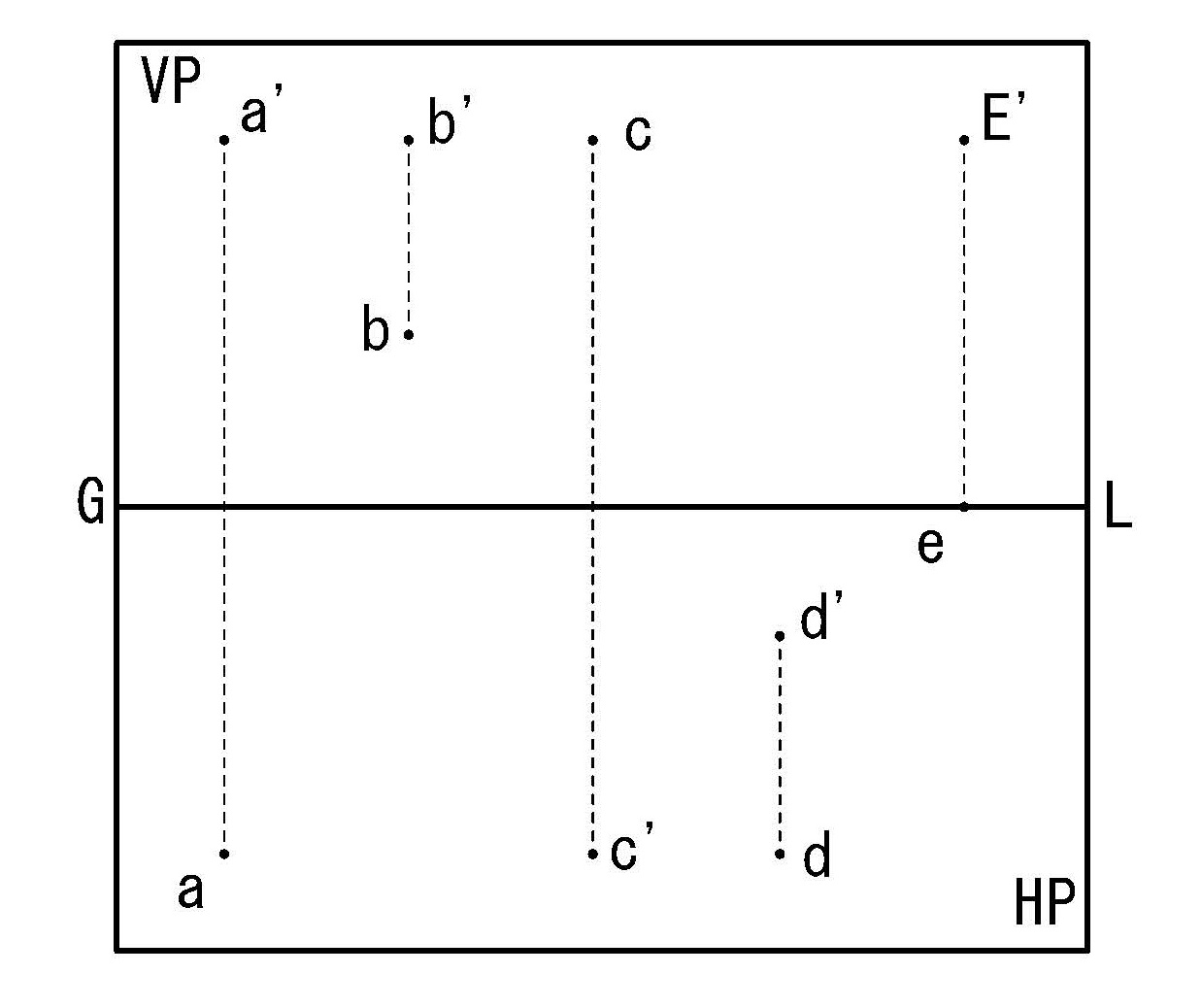
図4-2

【直線の表現】
点の作図と同様、図3-3（上図）のように点と点をまっすぐな線でつないだ線分は「複面投象」で作図すると図3-3（下図）のように表される。本来、直線とは幾何学ではどこまでもまっすぐ無限に伸びて端点を持たないものを意味し、有限の長さと両端を持つまっすぐな線は線分と呼ぶが、ここでは、線分をその端点（A,B）を明示して直線ABと表示する。水平面に垂直な直線DCの立面図c’d’は基線に垂直な線分となり、その平面図は１点c（又はd）となる。この状態を線分の点視図と呼ぶ。また直立面内にある直線EFの立面図e’f’は実形EFと重なるためE’F’と表し、その平面図efは基線上に表現される。

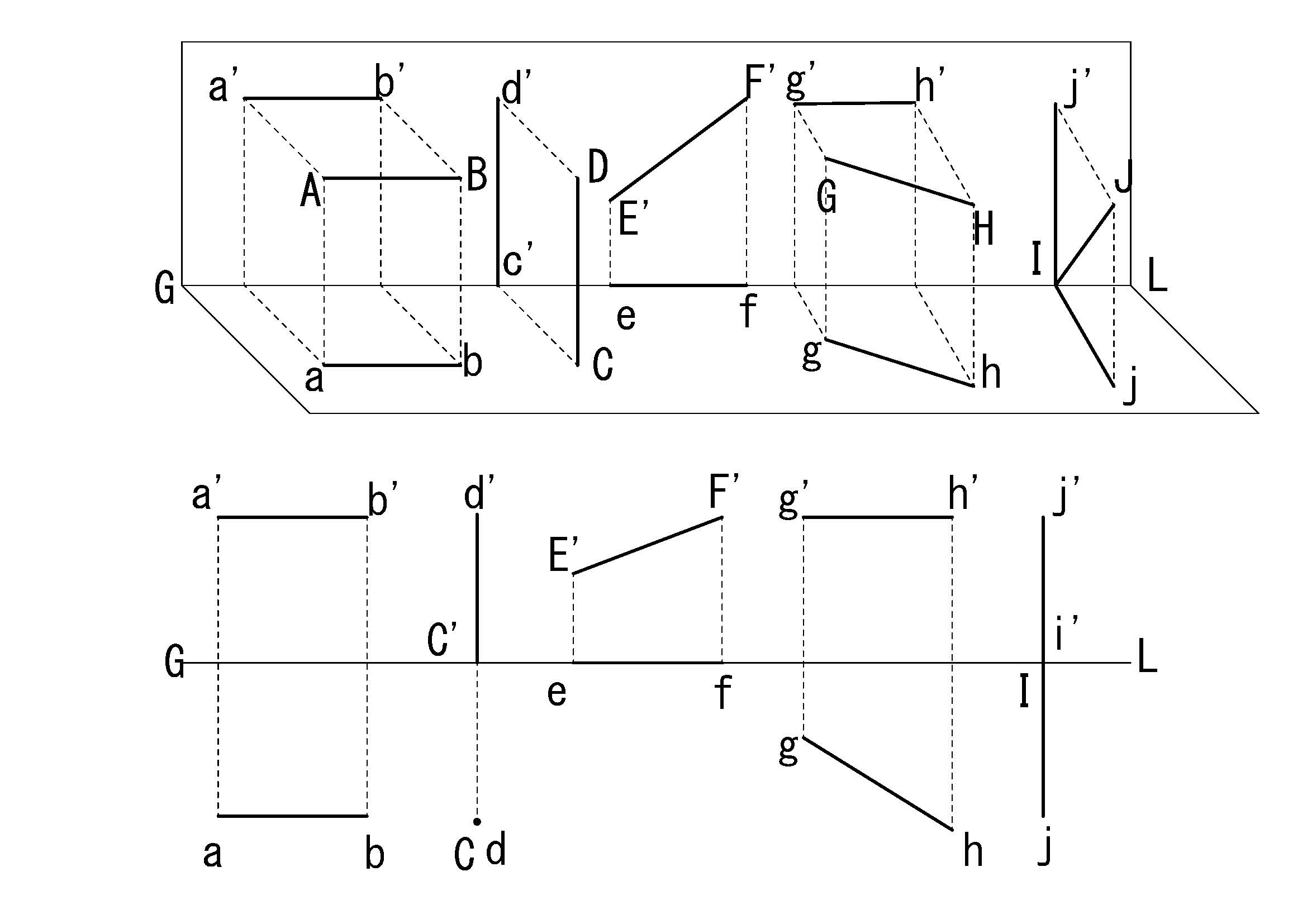
図4-3
CADデータ

図3-4のように空間内にある直線ABの両端を延長した時、直立面と交わる点Cを直立跡点、水平面と交わる点Dを水平跡点と呼ぶ。また直線ABと水平面とのなす角度を水平傾角、直立面とのなす角度を直立傾角と呼ぶ。

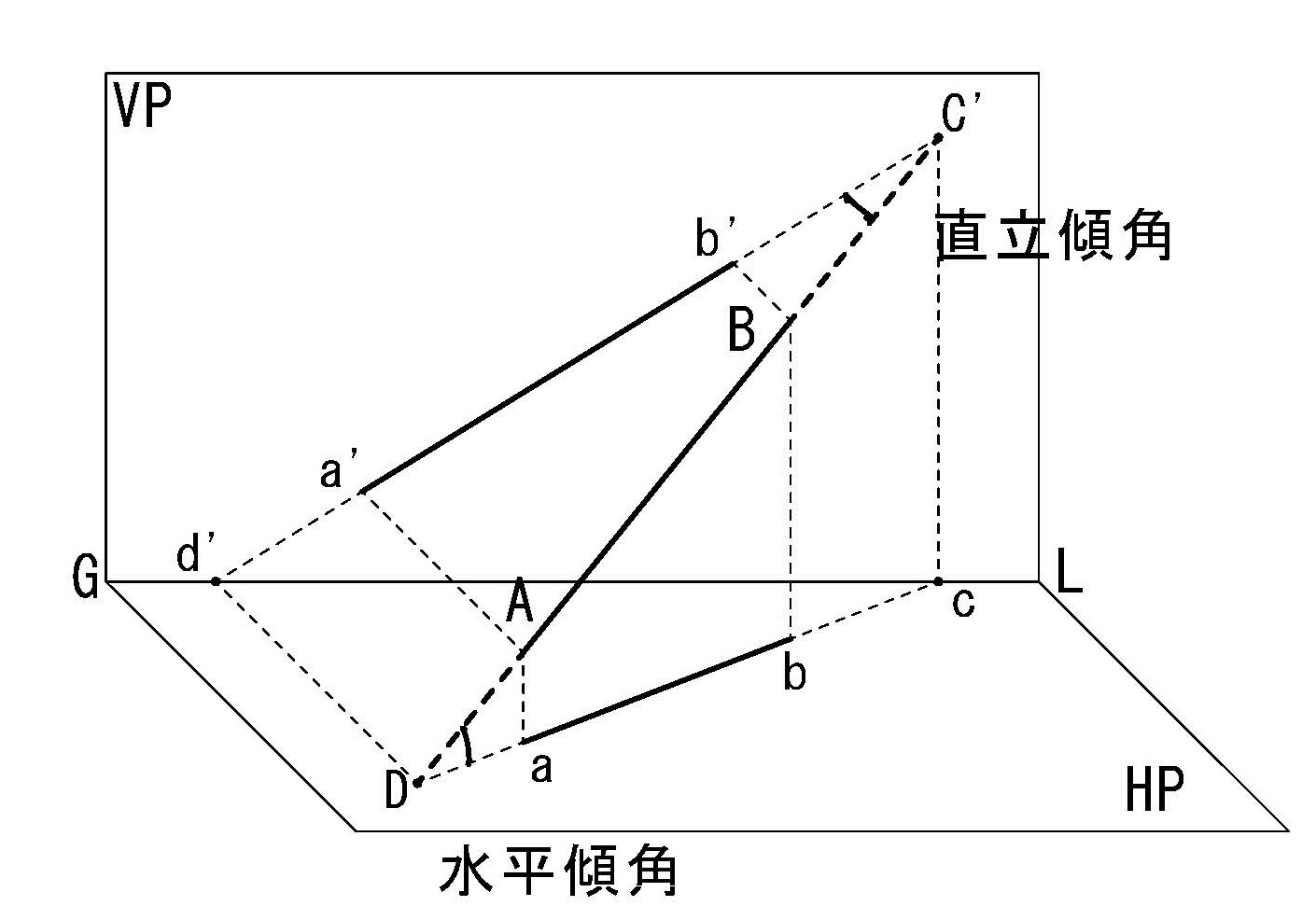
図4-4

【平面の表現】
平面は幾何学では平坦で無限の広さを持つものを意味し、広さが限定された平面図形とは区別する。図3-5のように空間内にある平面は「複面投象」ではそれが直立面と水平面と交差する交線によって図3-6のように表現する。この時、平面と水平面との交線を水平跡線、直立面との交線を直立跡線と呼ぶ。作図ではこの平面を大文字のＴで表し、その跡線は他の線と区別するために水平面では小文字のｔ、直立面では小文字のt’で表現する。また空間内で直立跡線と水平跡線のなす角度をその平面の開角と呼ぶ。ここで平面Tの開角θは複面投象で表された水平跡線と直立跡線のなす角度でないことに注意しておく必要がある。これは複面投象の立面図と平面図が基線GLを介して直角に交わっているためである。

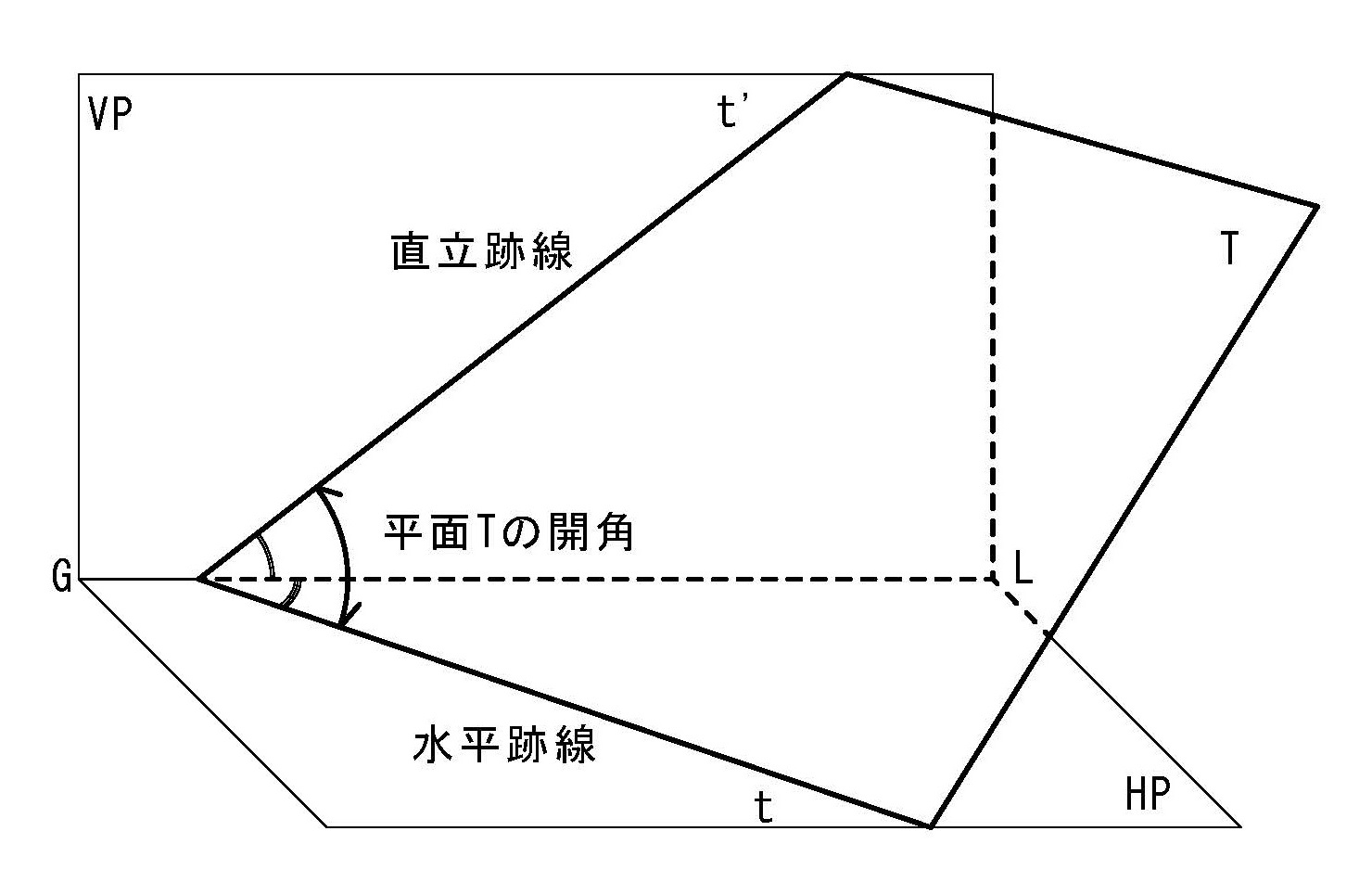
図4-5

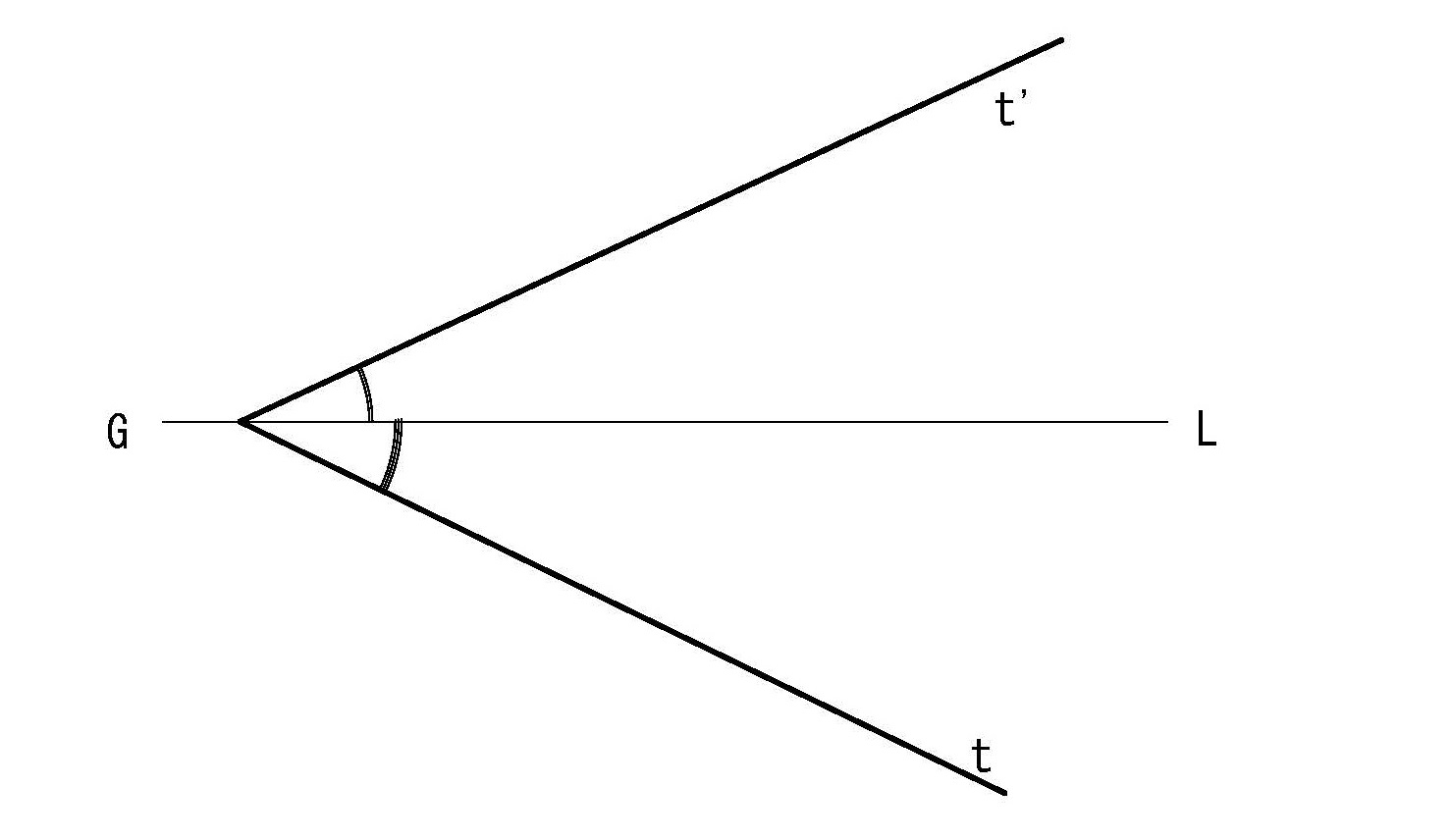
図4-6
図3-7は様々な平面の見取り図と複面投象を示している。平面T1は直立面に垂直な平面で複面投象ではその水平跡線が基線に垂直に示されており、平面T3は水平面に水平な平面で直立跡線は基線に平行で示され水平跡線は存在しない。

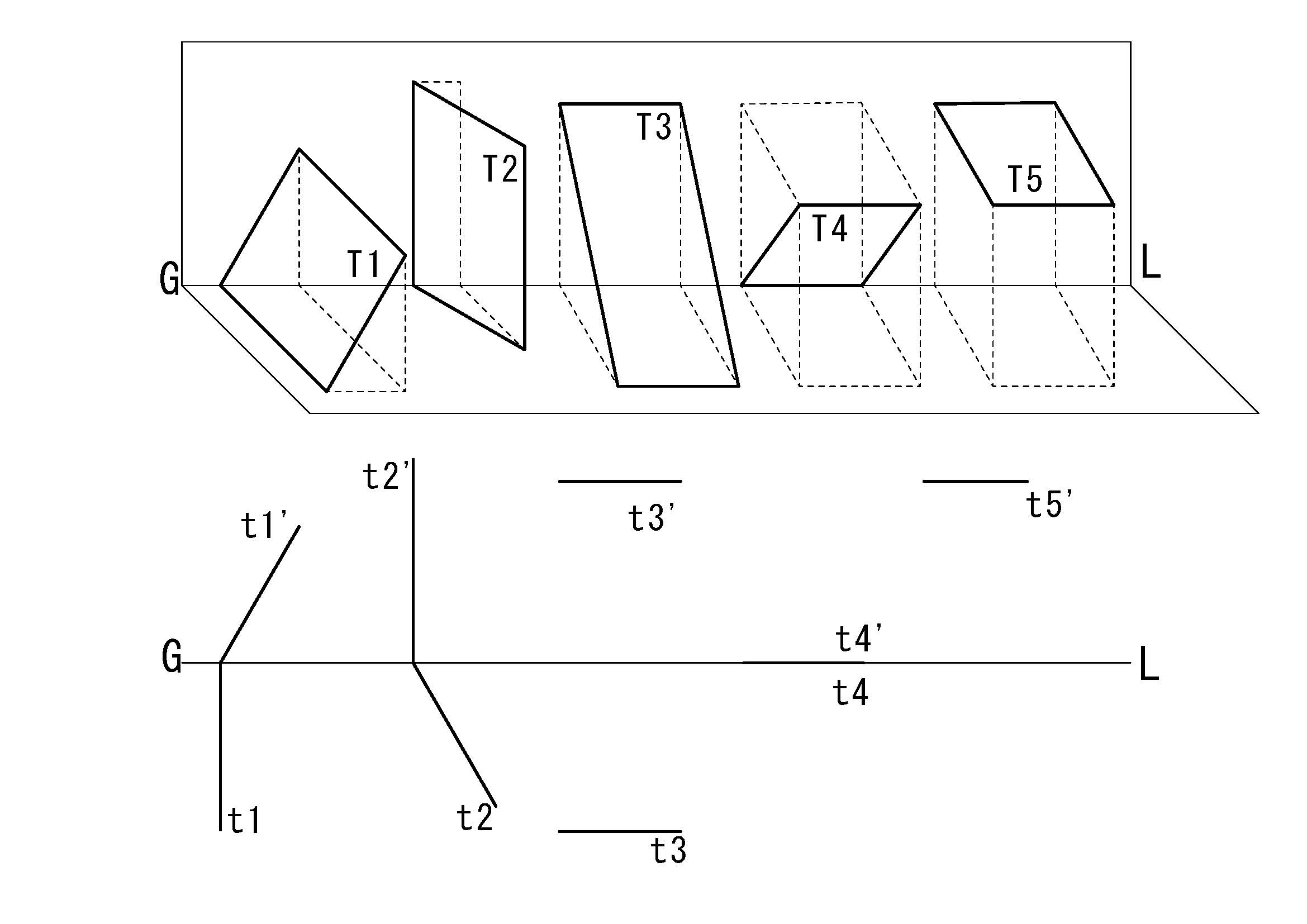
図4-7

【多面体の表現】
いくつかの平面で囲まれた立体を多面体とよび．立体を構成する平面を面、面と面の交線を稜、稜の集まる点を頂点、同一平面上にない2頂点を結ぶ直線を対角線と呼ぶ。同形同大の正多角形で囲まれ．各頂点に集まる稜の数が等しい凸多面体を正多面体とよび、図3-9の5種類が存在する。以下では多面体の代表として角柱と角錐の表現について解説する。

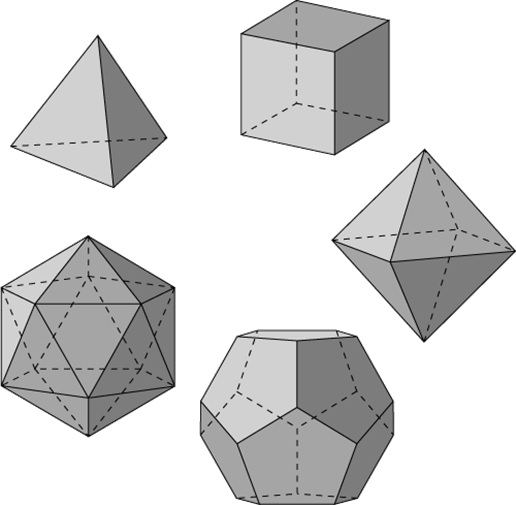
図4-8

【球の表現】
円が1つの直径を軸としてそのまわりに回転したとき生ずる曲面を球面と呼ぶ（図3-12b）。したがって球は回転面の一種としてとりあつかうことも出来るが．赤道を導円、経線を母線と考えれば複曲面である。

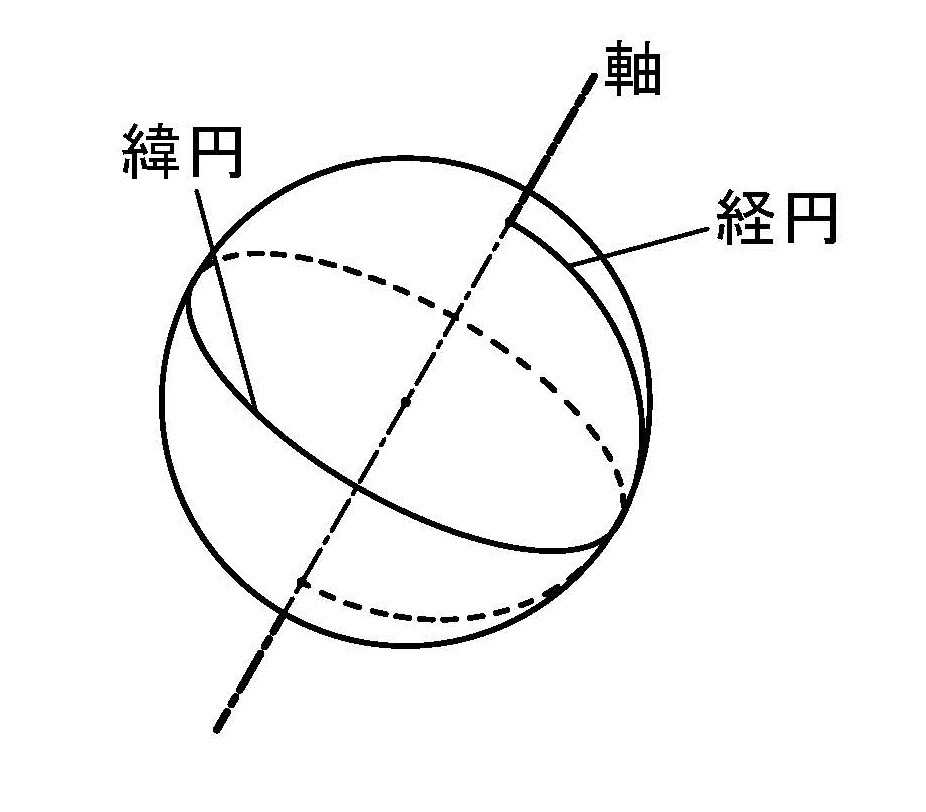
図4-11

【曲面の表現】
円錐面は1定点を通る直線が、ある円に沿って移動するとき生じる軌跡が作る曲面で、この時の定点を頂点、移動する直線を母線、移動するときに沿う円を導円と呼び、結果得られた曲面を円錐面と呼ぶ。ここで底面が円で円錐の軸がそれに垂直な場合を直円錐と呼び、それ以外は斜円錐と呼ぶ（図4-14）。

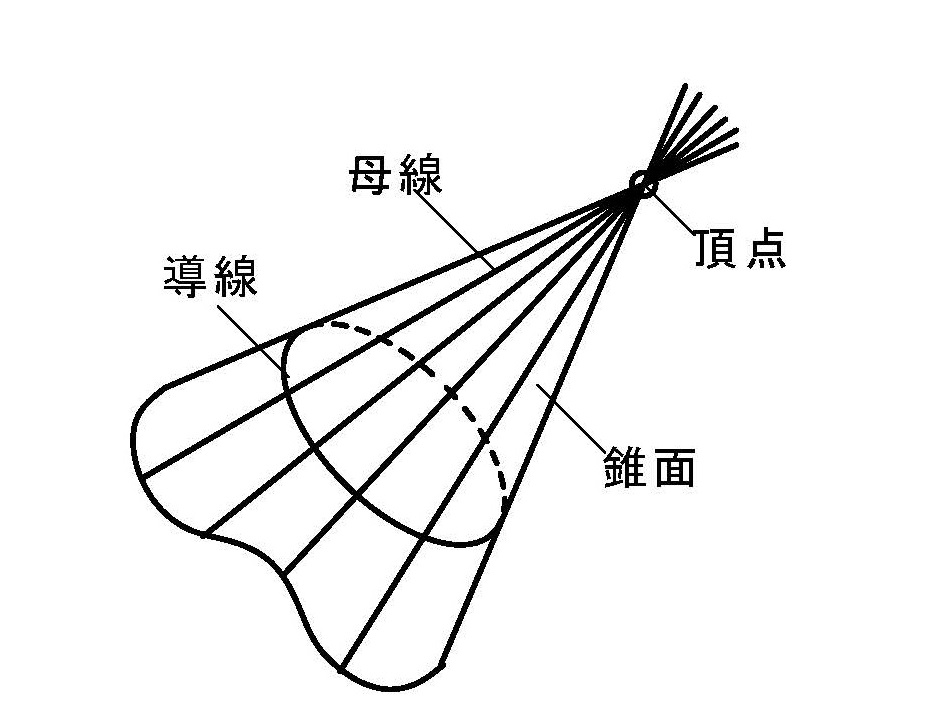
図4-13
【斜円錐】
図3-14のような空間内の水平面上に置かれた斜円錐VAの複面投象による作図は図3-14bのように平面図に斜円錐の底円Aと頂点v及びその頂点から底円への接線が斜円錐の外形線として示され、この斜円錐を水平面に対して垂直方向の真上から眺めた状態として、斜円錐の下側にある底円の一部は点線で示される。また立面図はこの斜円錐を直立面に対して垂直方向の真横から眺めた状態として、底面である円Aの線視図と外形線で示される。

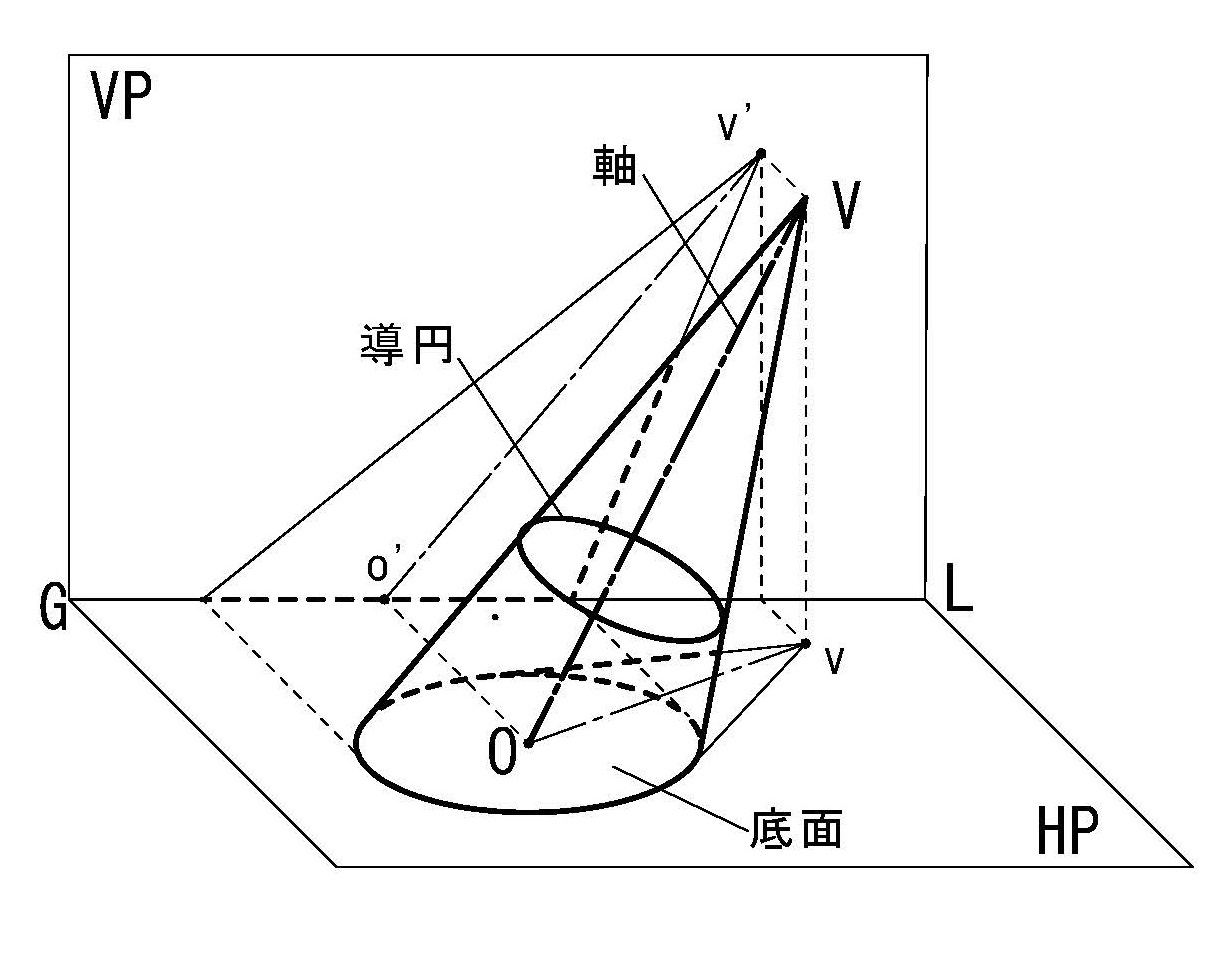
図4-14

【直円錐】
図3-15のような空間内に浮かぶ直円錐VAの複面投象による作図は図3-15bのように直円錐の頂点Vと直円錐に内接する球Oによって表現する。平面図、立面図では対応する頂点v、v’と球の外形線を示す円o、o’を描き、直円錐の外形線として頂点から円への接線を引くことで示される。

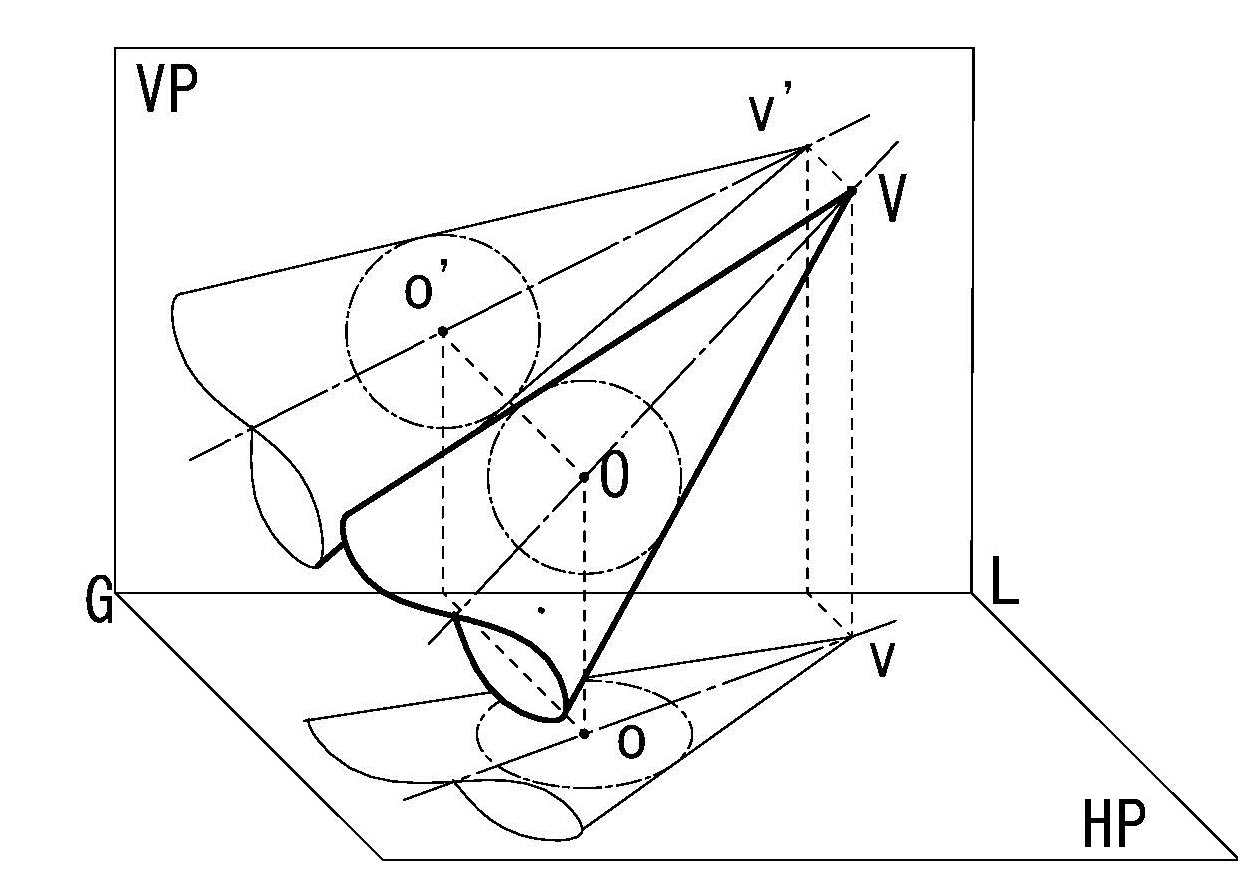
図4-15

4.2 要素図形の関係

【2直線の関係】
空間内の2つの直線がある時、それらの関係は「平行」、「交差」、「ねじれ」のいずれかの関係にある。図3-17において複面投象で表現された2直線ABとCDが平行であるためには、立面図における直線a’b’と直線c’d’平行であり、かつ平面図における直線abと直線cdも並行でなければならない。

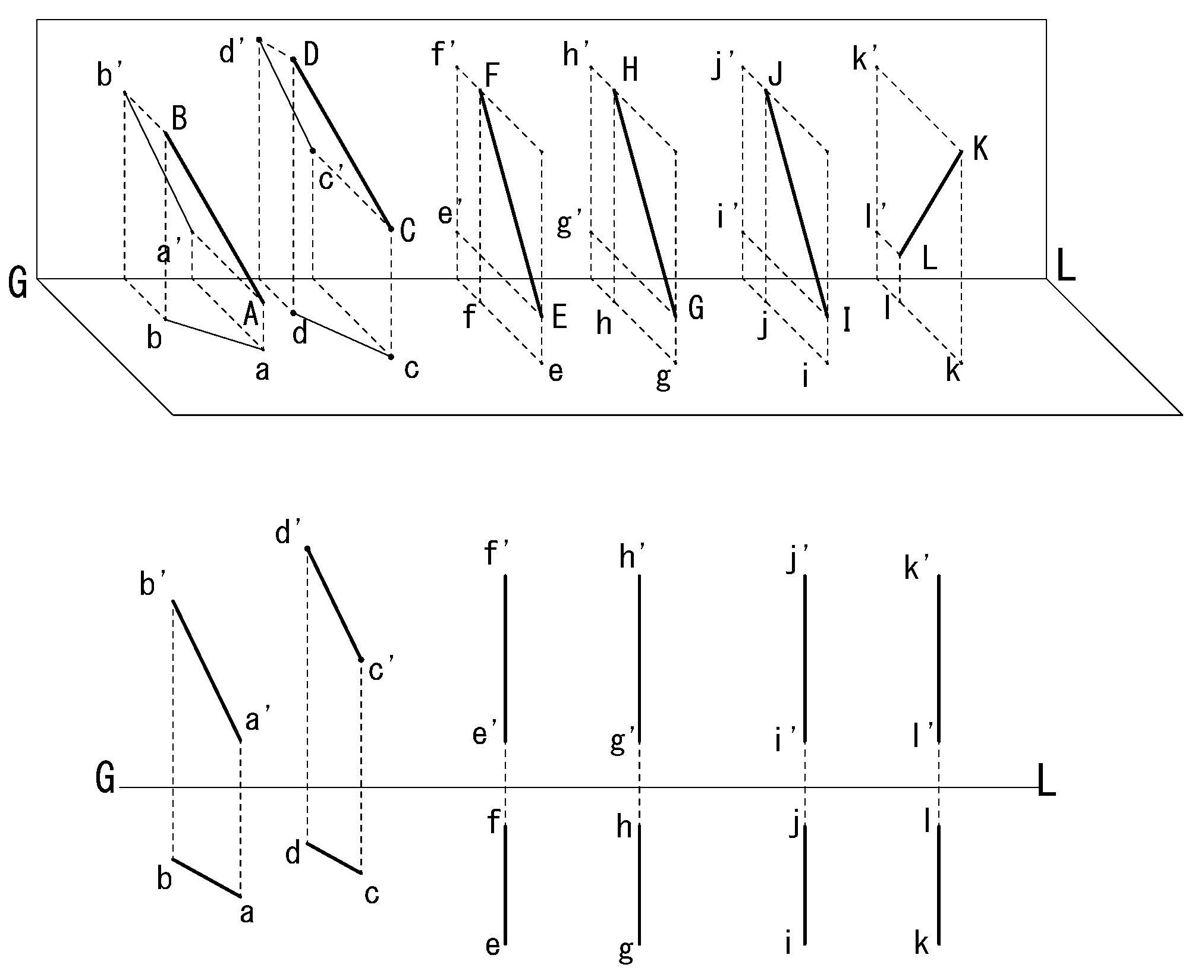
図4-17

【平面の関係】
空間内に2つの平面がある時、それらの関係は「平行」、「交差」のいずれかの関係にある。

作図題4-1
空間内にある平面T1と平面T2の交線を求めよ（図4-19）

図4-19
CADデータ

【平面と直線の関係】
空間内に平面と直線がある時、それらの関係は「平行」、「相貫」、「面内」のいずれかの関係にある。

作図題4-2
平面T1の面内に直線ABがあり、直線のABの立面図a’b’が与えられている時、直線ABの平面図求めよ（図4-20）

図4-20
CADデータ

4.3 図法の基本操作
【切断】

図法幾何学では立体の形状を明らかにしたり、その位置関係を求めるために、その立体を平面で切りとる操作を「切断」と呼び、その平面を「切断平面」、切り口を「断面」と呼ぶ。

図3-21（上図）は空間内にある平面T1を水平な切断平面T2で切断したもので、切り口（断面）は直線（切断線）となる。この切断線は水平であり高さは切断平面の高さと同じである。

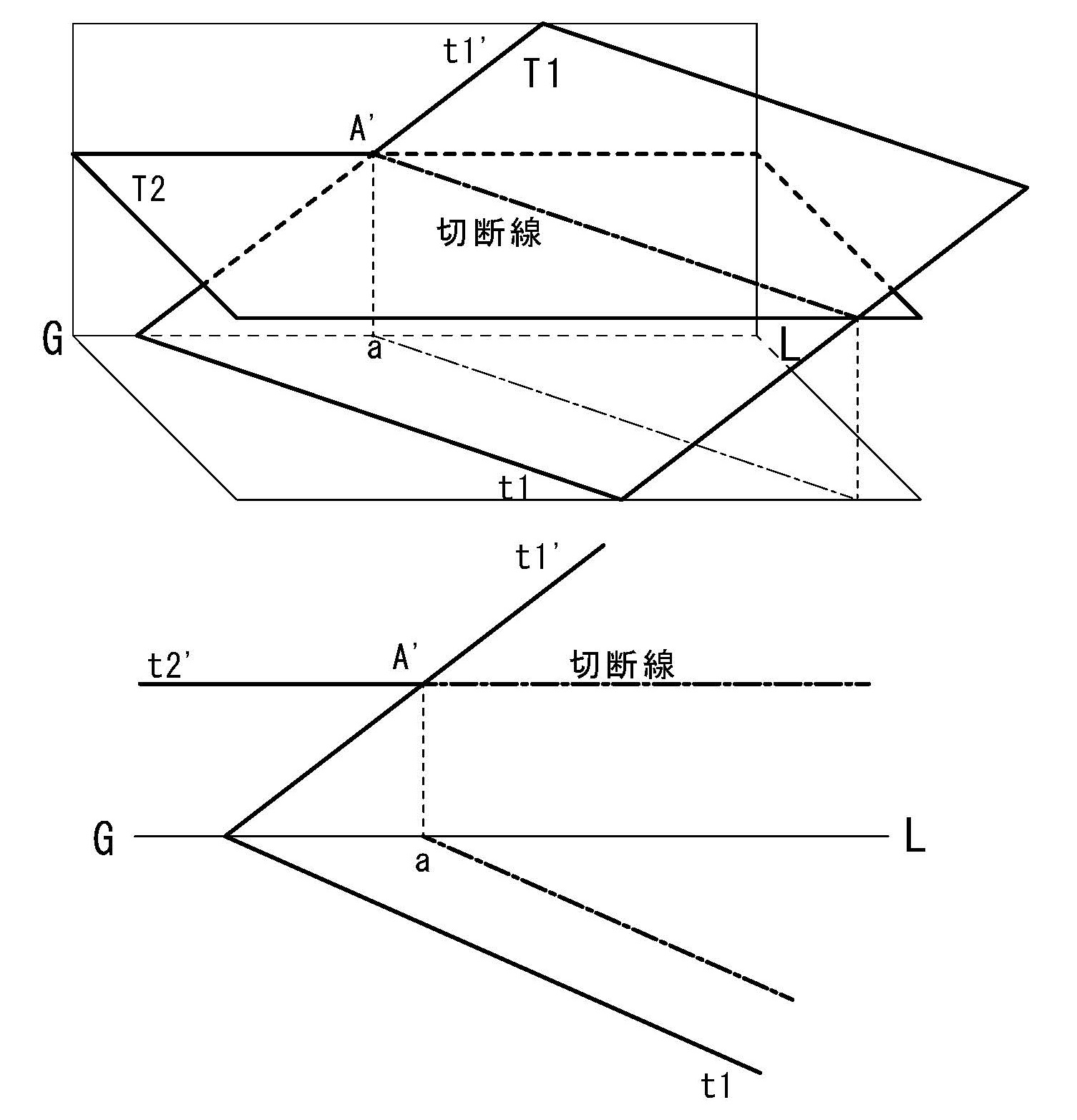
図4-21
これを複面投象（図4-21下図）で見ると立面図における平面T1の直立跡線t1’と切断平面T2の直立跡線t2’の交点A‘は直立面内にある。交点A’の平面図は直立面内であるため基線上の点aとなり、切断線の平面図は点aから平面T1の水平跡線に平行に示される。

作図題4-3【平面と直線の相貫】
空間内の平面T1と直線ABが交じわっている時、その相貫点を求めよ（図4-22）

図4-22
作図データ

作図題4-4【多角形と直線の相貫】
空間内にある三角形ABCと直線MNの相貫点を求めよ（図4-23）

図4-23
作図データ

作図題4-5【多面体と直線の相貫】
水平面上にある三角錐VABCと空間内にある直線MNの相貫点を求めよ（図4-24）

図4-24
作図データ

作図題4-6【多面体の相貫】
水平面上にある三角柱ABCDEFと三角錐VABCの相貫線を求めよ（図4-25）

図4-25
作図データ

【副投象】

副投象は複面投象の主投象面である直立面と水平面以外に、もう一つ別の方向から眺めた投象面（矢印の方向）を新たに作図して図形の形状や位置関係を把握するために用いる操作である。作図としては矢印の方向に直交する新たな基線（G’L’）を引き基線上の投象面（VP‘）を水平面上に回転させて表現する。

作図題4-7【多面体と平面の相貫】
水平面上にある三角錐VABCと空間内にある平面T1との相貫線を求めよ（図4-27）

図4-27
作図データ

作図題4-8【球と直線の相貫】
空間内にある球Oと直線MNとの相貫線を求めよ（図4-28）

図4-28
作図データ

作図題4-9【多角形の相貫】
空間内にある2つの三角形ABCとDEFの相貫線を求めよ（図4-29）

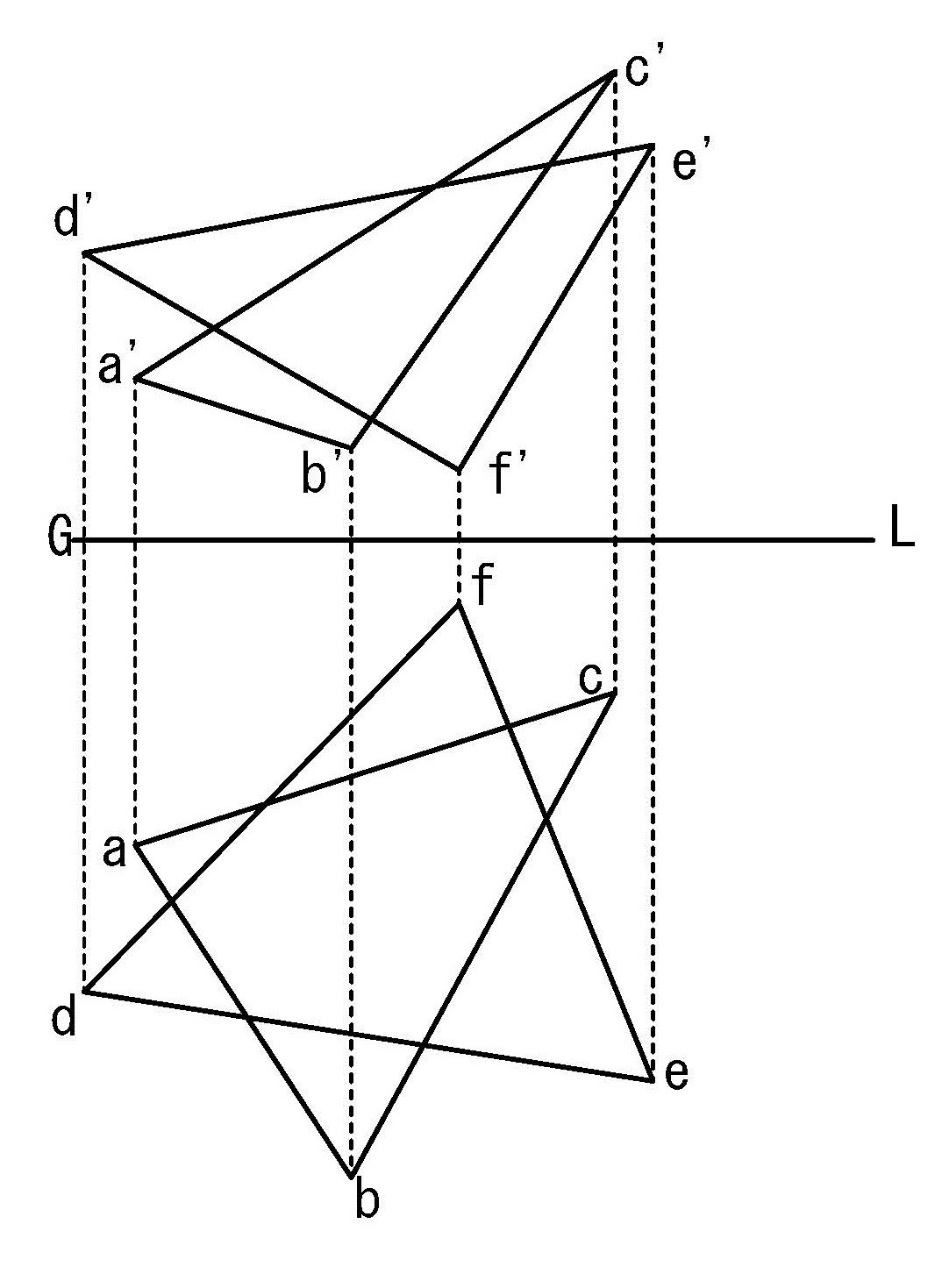
図4-29
作図データ

【回転】

空間内の図形を画面上の1直線を軸として回転させることでその図形の実形や切断面を把握するために行う操作である。例えば図3-34のように空間内にある直線ABの実長と水平傾角θを求めるためには直線ABの端点Bを通る垂直な直線を軸として直線ABが直立面に平行になるように回転させることによって直線ABの実長と水平傾角を求めることができる。

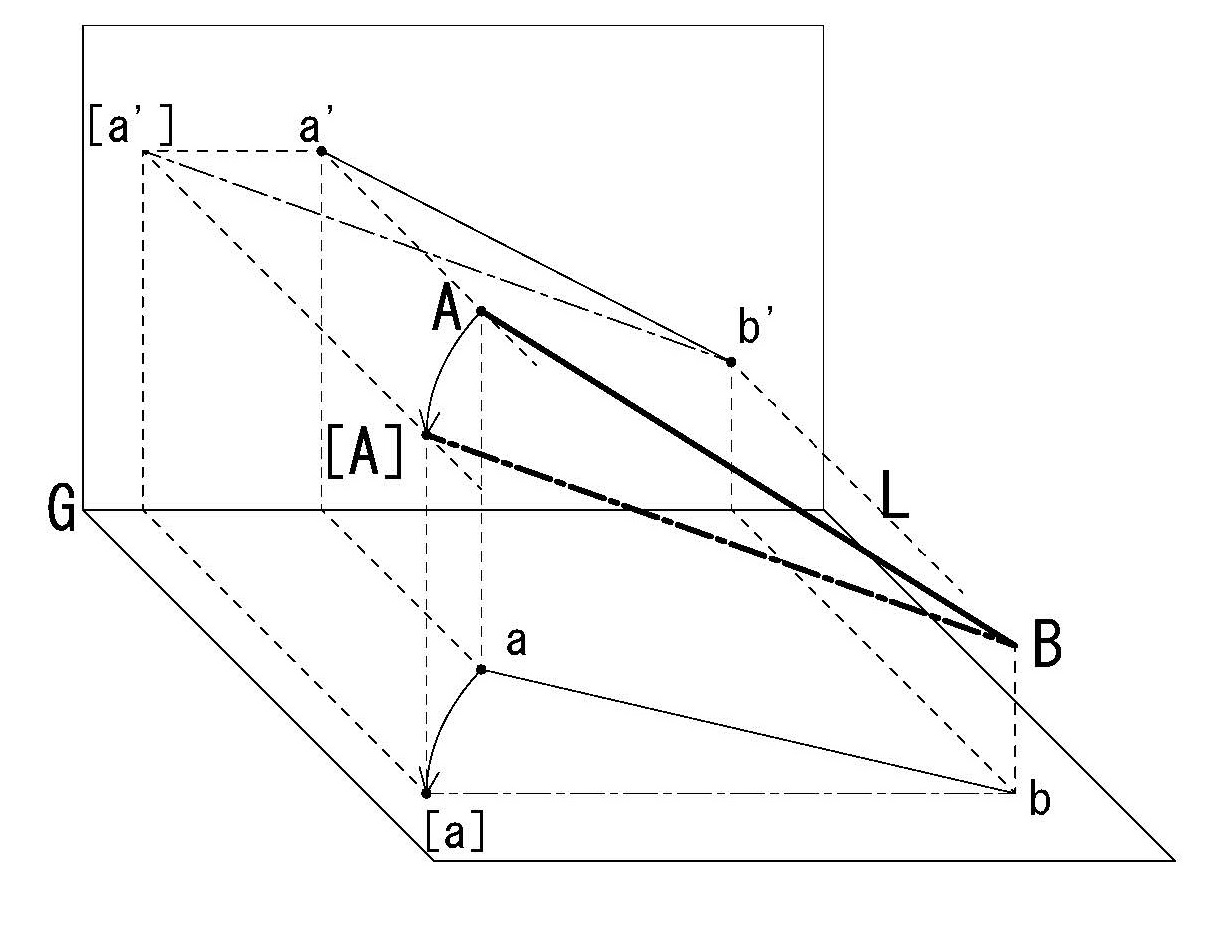
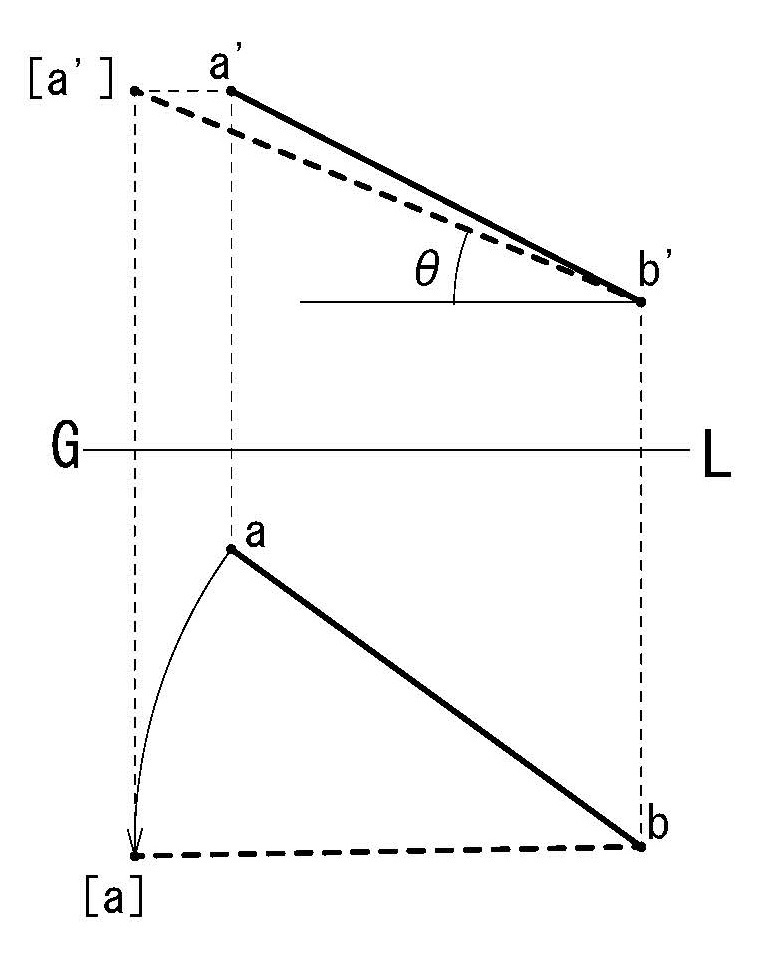
図4-30
図3-35は空間内にある平面Tの実形と開角αを求めるために、その水平跡線tを軸にして平面T（直立跡線t’）を水平面まで回転することで求めることができる。

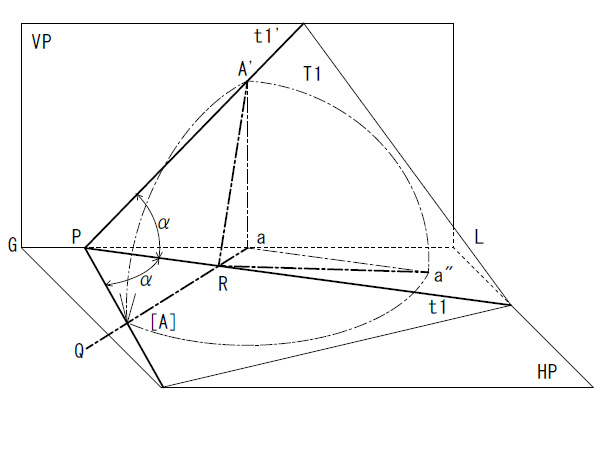
図4-31
作図データ

作図題4-10【多角形の実形】
空間内にあって直立面、水平面に平行でない三角形ABCの実形を求めよ（図4-32）

図4-32
作図データ

【陰影】

物体に光線が当たっている時、画面上に出来る物体のかげを影（Shadow）と呼び、物体の表面上に出来るかげを陰（Shade）と呼んで区別する。また光が空間上の「或る対象」に当たってできる影と「或る対象」を結ぶ直線をここでは影線と呼ぶ。また光線は平行光線と発散光線（点光源より出る光）の2種類があり、以下では平行光線において直立面、水平面に対してそれぞれ45°の角度になる平行光線を標準光線と呼ぶ（図4-33）。

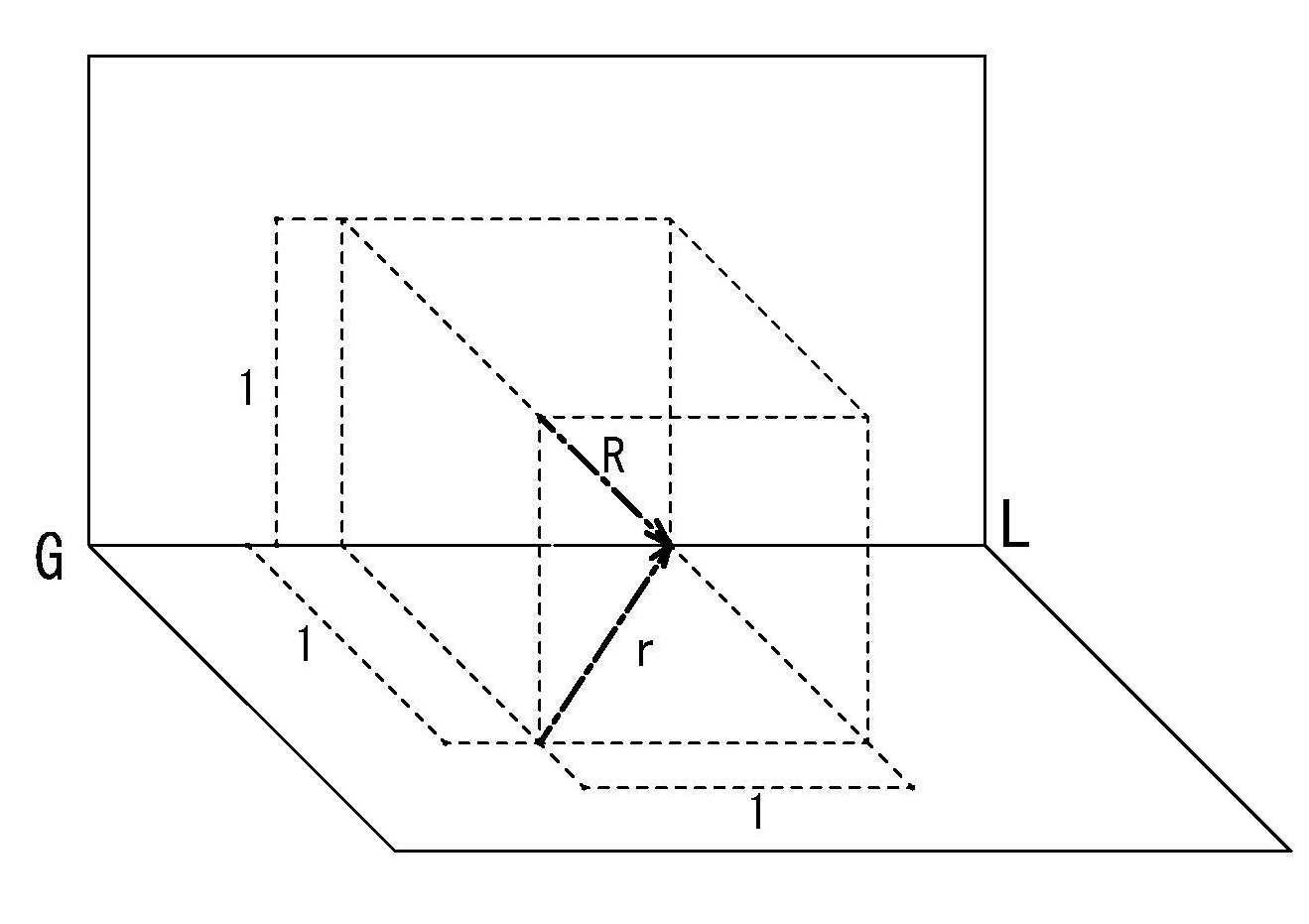
図4-33

作図題4-11【多面体の陰影】
平面上にある三角錐VABCに標準光線が当たっている時にできる陰影を求めよ（図4-34）

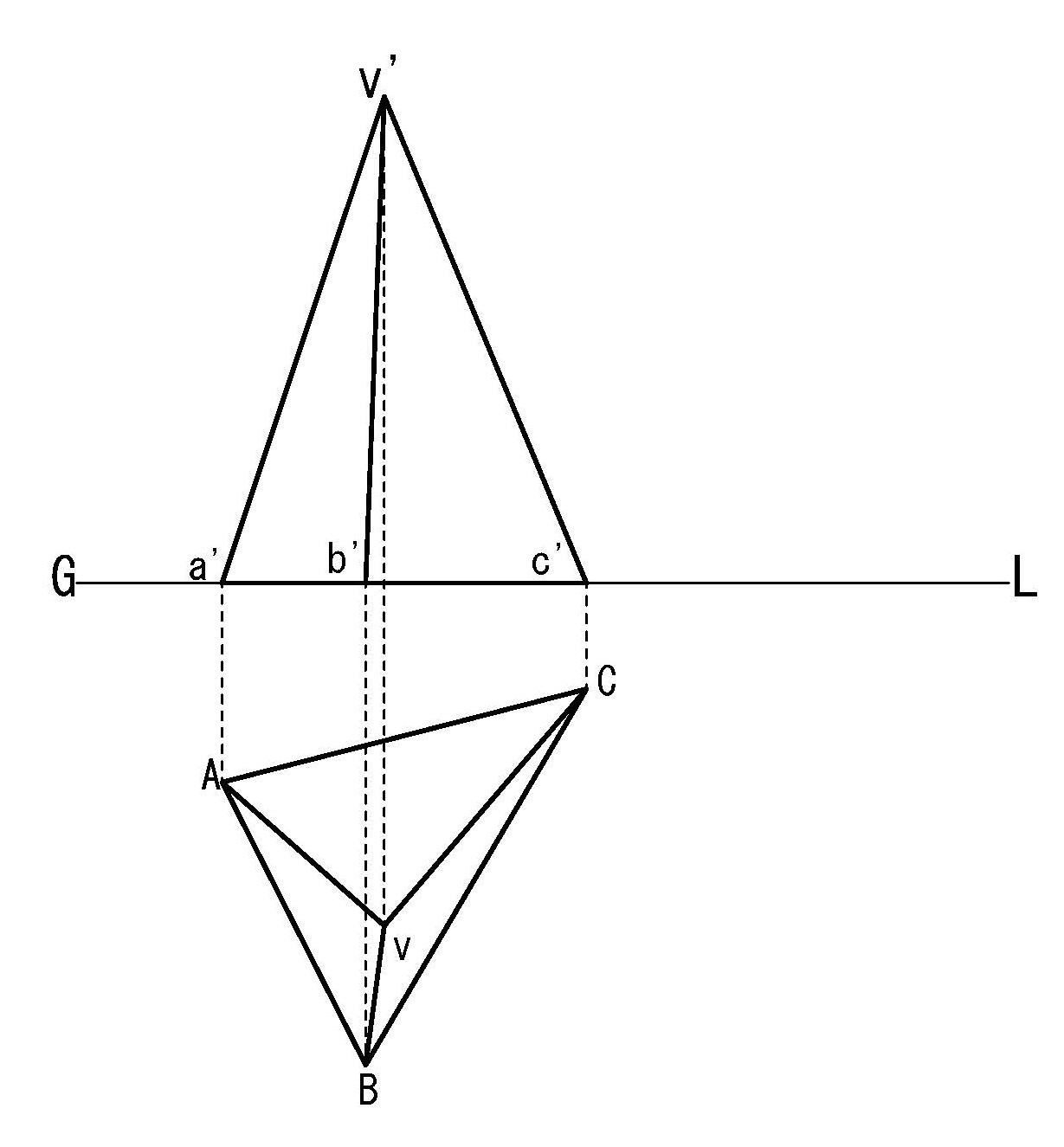
図4-34
作図データ

作図題4-12【球の陰影】
空間内にある球Oに標準光線が当たっている時にできる陰影を求めよ（図4-35）

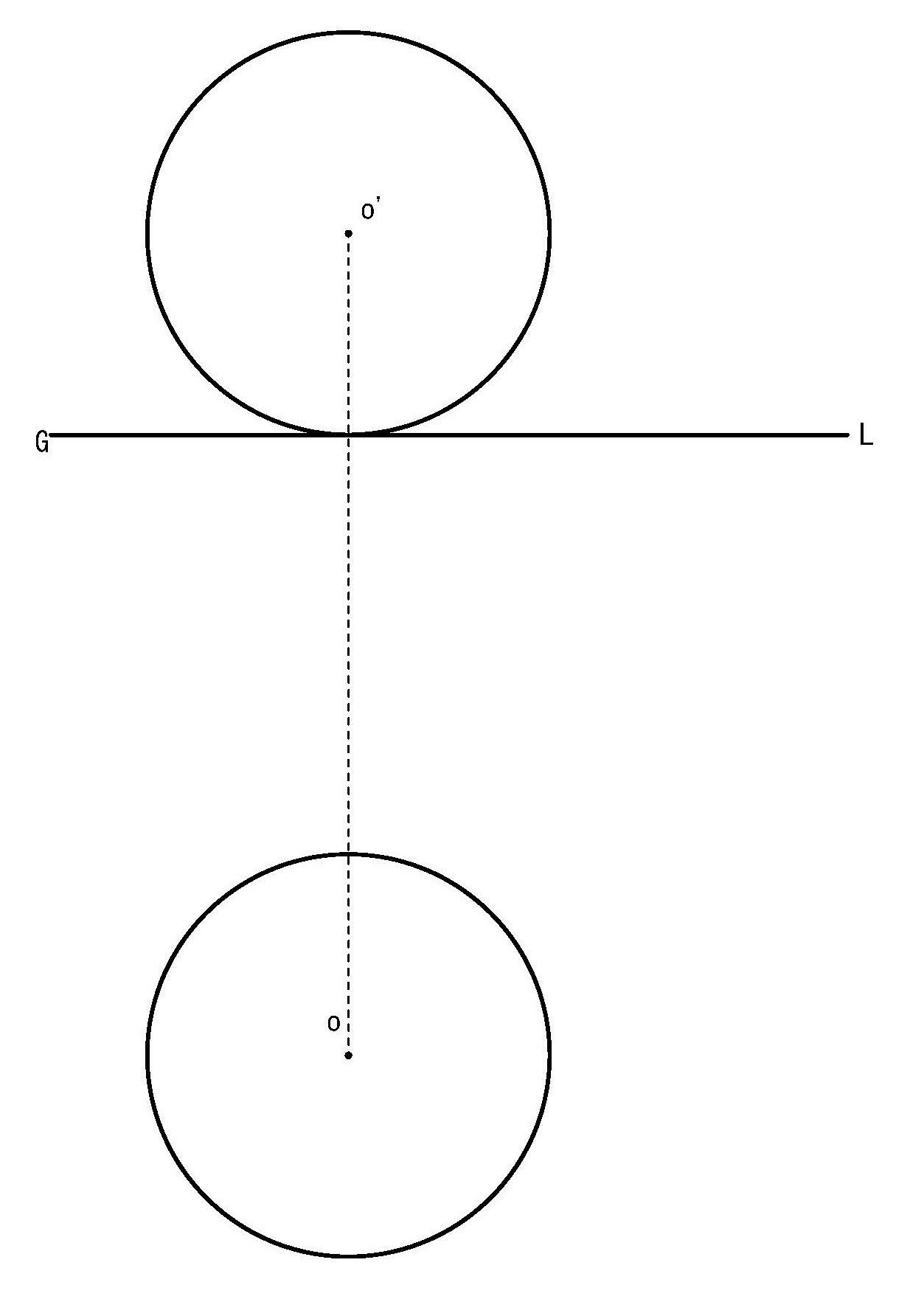
図4-35
作図データ

作図題4-13【点光源から直線への陰影】
空間内にある点Pから空間内にある2直線AB、CDの両方に交わる直線を求めよ（図4-36）

図4-36
作図データ

作図題4-14【斜円錐と直線の相貫】
水平面上にある斜円錐と直線の相貫点を求めよ（図4-37）

図4-37
作図データ

作図題4-15【直円錐と直線の相貫】
水平面上にある斜円錐と直線の相貫点を求めよ（図4-38）

図4-38
作図データ